MultiSecant vs. DIIS: A Practical Guide to Robust SCF Convergence for Surface Systems in Drug Development

Abstract

This article provides a comprehensive comparison of the MultiSecant and DIIS (Direct Inversion in the Iterative Subspace) methods for achieving Self-Consistent Field (SCF) convergence, with a specific focus on challenging surface systems relevant to computational drug development. We explore the foundational principles of SCF convergence challenges, detail the algorithmic workings and practical implementation of both methods, and offer advanced troubleshooting strategies for difficult cases like transition metal complexes. Through a systematic validation of their performance in terms of robustness, efficiency, and computational cost, this guide empowers researchers to select and optimize the right convergence accelerator for their biomedical simulations, ensuring reliable electronic structure calculations.

Understanding SCF Convergence: Why Surface Systems Pose a Unique Challenge

Frequently Asked Questions (FAQs)

Q1: What does the "SCF not converged" error mean, and why should I not ignore it? The "SCF not converged" error indicates that the self-consistent field procedure failed to find a stable electronic structure solution within the allowed iterations. Ignoring this error, for example by using commands that force the calculation to continue, is strongly discouraged as it can lead to physically meaningless and unreliable results for all subsequent calculation steps, including geometry optimizations, frequency analyses, and property calculations [1] [2].

Q2: What is the role of the orbital gradient in SCF convergence? The orbital gradient quantifies the rate of change of the total energy with respect to orbital rotations. It is a fundamental convergence criterion because a zero gradient indicates a stationary point on the electronic energy surface. Modern SCF algorithms, such as the Second-Order SCF (SOSCF) or the Trust Radius Augmented Hessian (TRAH) method, use the orbital gradient to construct efficient convergence paths. A large orbital gradient suggests the solution is far from a minimum, while a stagnating, non-zero gradient can indicate convergence difficulties [1] [3].

Q3: My calculation is for an open-shell transition metal complex and won't converge. Why are these systems so problematic? Open-shell transition metal complexes often pose SCF convergence challenges due to their high density of electronic states near the Fermi level, leading to a small HOMO-LUMO gap. This can cause excessive mixing between occupied and virtual orbitals during the SCF iterations. Furthermore, these systems may have multiple nearly degenerate electronic states, making it difficult for the algorithm to settle on a single solution [1] [4].

Q4: How does the DIIS method work, and when might it fail? The DIIS (Direct Inversion in the Iterative Subspace) method accelerates SCF convergence by extrapolating a new Fock matrix from a linear combination of Fock matrices from previous iterations, minimizing the error vector. DIIS can fail when the initial guess is poor, in systems with a small HOMO-LUMO gap, or when the error vector becomes ill-conditioned, leading to oscillations or divergence instead of convergence [1] [5]. This is where comparing DIIS with robust alternatives like MultiSecant or geometric direct minimization (GDM) methods becomes relevant for thesis research.

Q5: What is the fundamental difference between convergence criteria based on energy versus the density matrix? Energy-based criteria (e.g., TolE) focus on the change in total energy between cycles, while density-based criteria (e.g., TolRMSP, TolMaxP) monitor the change in the electron density matrix. ORCA's default behavior (ConvCheckMode=2) is a robust check of the change in both the total and one-electron energies. While the energy might stabilize, the density matrix might not have, which could signal an unconverged wavefunction. For most purposes, the energy-based check is efficient and sufficient, but for properties highly sensitive to the electron density, stricter, multi-criteria checks are recommended [3].

SCF Convergence Troubleshooting Guide

Initial Checks and Simple Fixes

Before applying advanced techniques, perform these basic checks.

• Verify Molecular Geometry: Ensure your molecular structure is reasonable. Unphysical bond lengths or angles can prevent convergence [4].
• Check Spin Multiplicity: Confirm that the correct number of unpaired electrons is specified for your system. An incorrect spin state is a common source of convergence failure [4].
• Increase SCF Iterations: If the SCF energy is steadily decreasing and nearly converged, simply increasing the maximum number of cycles can help.

• Loosen Convergence Criteria (Cautiously): For single-point energy calculations, slightly loosening the convergence criteria can sometimes help achieve numerical stability without significantly impacting the final energy.

Strategies for Difficult Systems

For stubborn cases, such as open-shell species or systems with small HOMO-LUMO gaps, a more strategic approach is required.

• Improve the Initial Guess:

  • Read Converged Orbitals: Converge a simpler calculation (e.g., with a smaller basis set or a different functional) and use its orbitals as the starting point for the more demanding job [1] [2].

  • Alternative Guess Algorithms: Switch from the default PModel guess to Hueckel or HCore [1].
  • Converge a Closed-Shell Ion: For an open-shell system, try to converge the SCF for its closed-shell cation or anion, then read those orbitals as the guess for the neutral species [1] [2].

• Algorithm Switching: DIIS, SOSCF, and Beyond:

  • Activate Second-Order Methods: If DIIS is oscillating or trailing off, enable the Second-Order SCF (SOSCF) algorithm, which uses orbital gradient information for more robust convergence [1].

  • Use Robust Convergers: For pathological systems, ORCA can automatically switch to the Trust Radius Augmented Hessian (TRAH) method, a powerful second-order converger [1] [3]. The KDIIS algorithm is another effective alternative [1].
  • Hybrid Approaches (GDM): As noted in Q-Chem documentation, a highly effective strategy is to use DIIS for the initial iterations and then switch to the Geometric Direct Minimization (GDM) method for final convergence, combining the strengths of both algorithms [5]. Research into MultiSecant methods explores similar hybrid strategies for improving convergence robustness.

• Advanced Technical Adjustments:

  • Damping and Level Shifting: For wildly oscillating SCF energies, use damping (! SlowConv/! VerySlowConv) or apply a level shift to virtual orbitals to increase the HOMO-LUMO gap artificially, reducing orbital mixing [1] [2] [4].
  • Increase DIIS Subspace: For difficult systems, increasing the number of previous Fock matrices used in the DIIS extrapolation can stabilize convergence [1] [5].

  • Fock Matrix Rebuild: In cases with significant numerical noise (e.g., when using diffuse basis sets), increasing the frequency of the full Fock matrix rebuild (directresetfreq) can aid convergence [1].

Diagnostic Table and Guide

The table below summarizes common SCF failure symptoms and recommended actions.

Symptom	Possible Cause	Recommended Action
Steady but slow convergence	Insufficient cycles	Increase MaxIter [1]
Large initial oscillations	Poor initial guess, small HOMO-LUMO gap	Use Guess Huckel, MORead, or apply SlowConv/level shifting [1] [2] [4]
Convergence "trailing off" (DIIS failure)	Ill-conditioned DIIS extrapolation	Switch on SOSCF, use KDIIS, or enable TRAH [1]
SOSCF fails with "huge step" error	Orbital gradient is too large for SOSCF	Delay SOSCF startup with SOSCFStart 0.00033 [1]
Convergence fails with diffuse functions	Numerical linear dependence/noise	Use a larger integration grid, set directresetfreq 1 [1] [2]

Workflow for Systematic Troubleshooting

The following diagram outlines a logical, step-by-step procedure for diagnosing and resolving SCF convergence issues.

Research Reagent Solutions: A Computational Toolkit

The table below lists key "reagents" – computational methods and input parameters – essential for handling SCF convergence in research.

Research Reagent	Function / Purpose	Example Use Case
SOSCF	Second-Order SCF algorithm; uses orbital gradient for robust convergence when near a solution.	Resolving final convergence when DIIS trails off [1].
TRAH	Trust Radius Augmented Hessian; a powerful, automatic fall-back converger in ORCA.	Difficult open-shell transition metal complexes where default DIIS fails [1] [3].
KDIIS	An alternative SCF acceleration algorithm.	Can provide faster convergence for some systems compared to standard DIIS [1].
LevelShift	Artificially increases energy of virtual orbitals.	Suppressing oscillation in systems with a small HOMO-LUMO gap [2] [4].
MORead	Reads orbitals from a previous calculation as the initial guess.	Providing a high-quality starting point from a converged, related calculation [1] [2].
DIISMaxEq	Controls the number of previous Fock matrices used in DIIS extrapolation.	Stabilizing DIIS for pathological cases (e.g., metal clusters) [1].
SlowConv	Applies damping to the SCF procedure.	Calming large oscillations in the initial SCF iterations [1].
2-(5-Nitropyridin-2-YL)ethanamine	2-(5-Nitropyridin-2-YL)ethanamine, CAS:503540-39-4, MF:C7H9N3O2, MW:167.17 g/mol	Chemical Reagent
4-(3-Chloro-4-fluorophenyl)aniline	4-(3-Chloro-4-fluorophenyl)aniline, CAS:405058-02-8, MF:C12H9ClFN, MW:221.66 g/mol	Chemical Reagent

Quantitative SCF Convergence Criteria

Precise control over SCF convergence is critical. The following table summarizes the standard convergence tolerance sets available in ORCA, which define the thresholds for the energy change, orbital gradient, and density change that must be met for the calculation to be considered converged [3].

Convergence Level	TolE (Energy)	TolRMSP (Density)	TolG (Orbital Gradient)	Typical Application
LooseSCF	1e-5	1e-4	1e-4	Initial geometry scans, preliminary tests.
Normal (Default)	~1e-6	~1e-6	~5e-5	Standard single-point energies, routine geometry optimizations.
TightSCF	1e-8	5e-9	1e-5	High-accuracy single-points, transition metal complexes, property calculations.
VeryTightSCF	1e-9	1e-9	2e-6	Benchmark calculations, sensitive property analysis.
ExtremeSCF	1e-14	1e-14	1e-9	Pushing convergence to numerical limits (rarely needed).

FAQs: SCF Convergence in Surface Systems

1. Why do my SCF calculations for metallic or small-gap surface systems fail to converge?

Systems with zero or small HOMO-LUMO gaps (like metals) exhibit very slow convergence or total failure because the energetic ordering of orbitals can switch during SCF optimization, creating discontinuities [6]. This is common in surface systems where delocalized electrons create nearly degenerate states around the Fermi level.

2. What makes open-shell transition metal complexes on surfaces particularly challenging for SCF convergence?

Open-shell configurations in transition metal complexes feature localized open-shell configurations that create multiple nearly degenerate states [4]. The strong fluctuation of SCF errors during iteration may indicate an electronic configuration far from any stationary point or an improper description by the approximation used [4].

3. When should I choose MultiSecant over DIIS for surface system calculations?

MultiSecant can be tried as an alternative at no extra cost per SCF cycle when experiencing convergence problems [7]. DIIS can become unstable for systems with small gaps or strong electron correlation, while MultiSecant approaches may offer more stable convergence for these problematic cases.

4. How does electron smearing help with small-gap systems, and what are its drawbacks?

Electron smearing uses fractional occupation numbers to distribute electrons over multiple near-degenerate levels, preventing oscillatory behavior [4] [6]. However, it alters the system's total energy, so the parameter should be kept as low as possible, ideally using multiple restarts with successively smaller values [4].

Troubleshooting Guides

Problem: Small HOMO-LUMO Gap Systems

Diagnosis: Common in metallic systems, surfaces with delocalized states, and systems with nearly degenerate frontier orbitals.

Solutions:

• Implement Electron Smearing: Use pseudo-Fractional Occupation Number (pFON) methods with Fermi-Dirac distribution [6].

• Typical pFON Parameters:

  • FON_T_START: 300-1000 K (electronic temperature)
  • FON_NORB: Number of valence orbitals (typically 4-10)
  • FON_E_THRESH: Set to 5 (freeze occupations when DIIS error < 10⁻⁵)

• Alternative Approach: Level shifting artificially raises the energy of unoccupied levels but may give incorrect values for properties involving virtual levels [4].

Problem: Open-Shell Configurations

Diagnosis: Common in transition metal surface complexes, radical adsorbates, and systems with dissociating bonds.

Solutions:

• Verify Spin Multiplicity: Ensure correct spin multiplicity is used. Open-shell systems should be computed with spin-unrestricted formalism [4].
• Initial Spin Breaking: Use VSplit to add a constant to the beta spin potential at startup (default 0.05) or StartWithMaxSpin to occupy numerical orbitals in maximum spin configuration [7].
• Spin Flip Techniques: Use SpinFlip for specific atoms to distinguish between ferromagnetic and antiferromagnetic states [7].

Problem: General SCF Convergence Failure

Diagnosis: Oscillating energies, non-decreasing DIIS error, or sudden divergence.

Solutions:

• Stabilize DIIS:

  • Increase DIIS expansion vectors (N=25 instead of default 10)
  • Delay DIIS start (Cyc=30 instead of 5)
  • Reduce mixing parameter (Mixing=0.015 instead of 0.075-0.2) [4] [7]

• Alternative Algorithms: Switch to MESA, LISTi, EDIIS, or ARH methods [4].

• Tighten Convergence Criteria Gradually: Use tighter thresholds only after initial convergence [3].

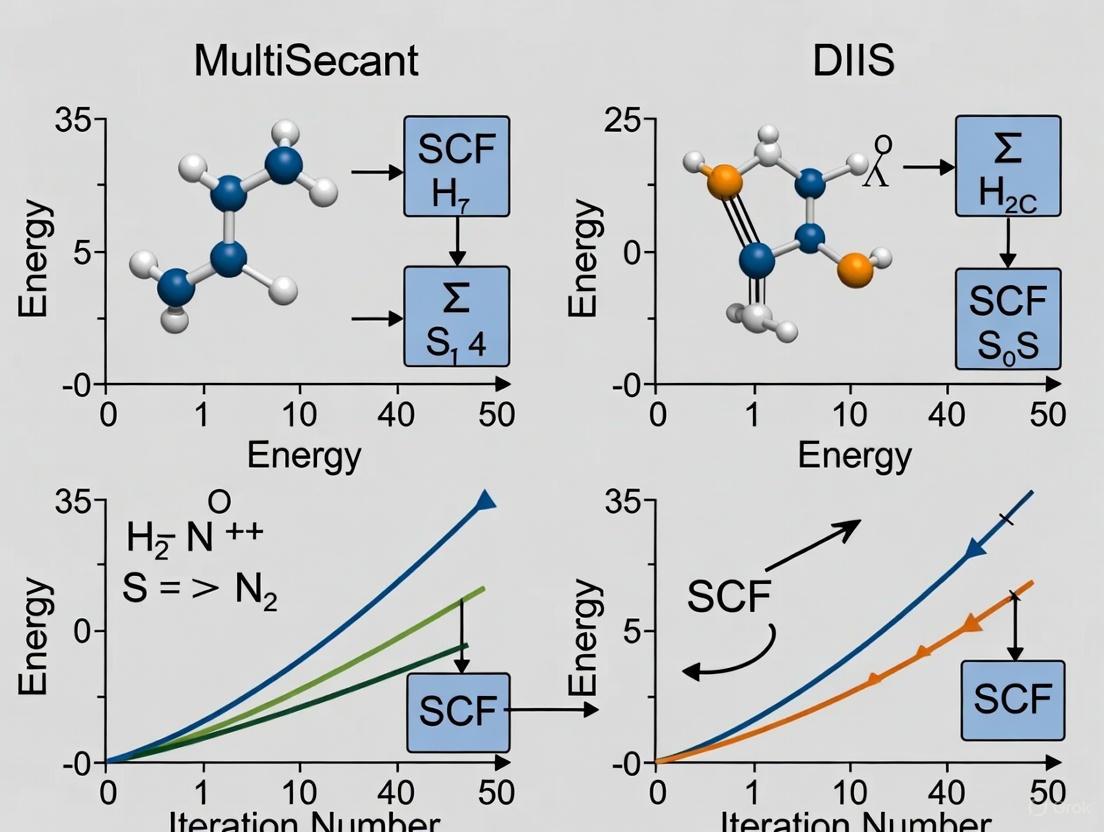
Method Comparison: MultiSecant vs. DIIS

Table 1: Comparison of SCF Convergence Acceleration Methods for Surface Systems

Parameter	DIIS	MultiSecant	MultiStepper
Default in	ADF	BAND	BAND
Stability for small gaps	Poor [6]	Good [7]	Flexible [7]
Memory usage	Higher (stores N vectors)	Moderate	Variable
User control	Extensive parameters [4]	Limited	Preset paths [7]
Best for	Well-behaved systems	Problematic cases [7]	Default use
Key parameters	N (expansion vectors), Cyc (start cycle), Mixing	Rate (convergence rate)	Preset path

Table 2: Recommended DIIS Parameters for Difficult Surface Systems

Parameter	Default Value	Stable Setting	Effect
N	10	25	More stable iteration
Cyc	5	30	More initial equilibration
Mixing	0.075-0.2	0.015	More conservative updates
Mixing1	0.2	0.09	Slower initial convergence

Experimental Protocols

Protocol 1: pFON for Metallic Surface Systems

Based on Q-Chem's implementation for small-gap systems [6]:

• Start with moderate temperature (300-500 K)
• Use constant temperature for initial attempts
• Gradually cool if needed: FONTSTART > FONTEND
• Monitor occupation numbers to ensure smooth convergence

Protocol 2: Stable DIIS for Open-Shell Complexes

Example input for difficult open-shell surface systems [4]:

• Begin with conservative mixing parameters
• Increase number of DIIS expansion vectors
• Delay DIIS start to allow initial equilibration
• For severe cases, disable DIIS initially (N<2)

Workflow Visualization

SCF Convergence Troubleshooting Workflow

Research Reagent Solutions

Table 3: Computational Tools for Surface System Convergence

Tool/Method	Function	Typical Use Case
Electron Smearing (pFON)	Enables fractional orbital occupations	Metallic surfaces, small-gap systems [6]
Spin Breaking (VSplit)	Breaks initial spin symmetry	Open-shell transition metal complexes [7]
ARH Method	Direct energy minimization using preconditioned conjugate-gradient	Systems where DIIS fails completely [4]
MultiSecant	Alternative convergence acceleration	Problematic cases where DIIS fails [7]
Level Shifting	Artificially raises virtual orbital energies	Emergency stabilization (alters results) [4]
autoSKZCAM Framework	Multilevel embedding for correlated wavefunction theory	High-accuracy surface chemistry predictions [8]

FAQs on SCF Convergence and Initial Guesses

Q: Why is the initial guess so critical for SCF convergence in surface systems and transition metal complexes? Systems like metal clusters and surfaces often have very small energy gaps between the highest occupied and lowest unoccupied molecular orbitals (HOMO-LUMO gap) [9]. This can lead to charge sloshing—a long-wavelength oscillation of charge density during the SCF process—making convergence difficult [9]. A poor initial guess can exacerbate these oscillations, causing the calculation to diverge or stagnate.

Q: What specific strategies can I use to generate a better initial guess? For difficult cases, avoid relying solely on the default initial guess. Several strategies can be employed:

• Use a Core Hamiltonian: Specify guess=core in Gaussian to use a simple core Hamiltonian, which can sometimes be more stable than the default for problematic systems [2] [10].
• Hückel or INDO Methods: Employ guess=huckel or guess=indo to use semi-empirical methods for generating the initial guess, which can provide a better starting point than the default [2].
• Exploit Fragment Convergence: If your system is a cation or a closed-shell species that is easier to converge, run that calculation first. Then, use guess=read to read the resulting molecular orbitals as the initial guess for the target open-shell or neutral system [2].

Q: My calculation uses a Minnesota functional (e.g., M06-2X) and won't converge. What should I check? The integration grid accuracy is crucial for these functionals. Ensure you are using a fine grid, such as int=ultrafine in Gaussian 16. Using the same grid for all calculations you intend to compare is essential for consistent energies [2].

Q: What is the most robust SCF method for metallic systems when DIIS fails? The Quadratic Convergent SCF (QC-SCF) method is considered robust and reliable for these systems, though it is computationally more expensive [9]. As an alternative, the MultiSecant method is a powerful option that comes at no extra cost per SCF cycle compared to DIIS and is often successful where DIIS fails [11].

Troubleshooting Guide: SCF Convergence Issues

Follow this logical workflow to diagnose and solve SCF convergence problems.

Detailed Troubleshooting Protocols

Step 1: Check Input & Geometry Before adjusting SCF parameters, eliminate simple errors. Incorrect atomic coordinates, unit mismatches (e.g., Bohr vs. Angstrom), or incorrectly specified molecular charge and spin are common culprits. A bad molecular geometry, such as unrealistic bond lengths or angles, can also prevent convergence [10].

Step 2: Improve the Initial Guess If the default guess fails, proceed with these methods:

• Protocol for guess=read from a Smaller Basis Set: First, run a single-point energy calculation on the same geometry using a minimal basis set (e.g., STO-3G). Once this calculation converges, start a new calculation with your target larger basis set and functional, using the keyword guess=read to use the orbitals from the previous job as the starting point [11] [2].
• Protocol for guess=read from an Ionized System: For a difficult-to-converge open-shell system, first run a calculation on its corresponding cation (which often has a larger HOMO-LUMO gap). After convergence, use guess=read in the input for the neutral open-shell system to read the cation's orbitals [2].

Step 3: Apply Convergence Aids These techniques help dampen oscillations in the density.

• Energy Level Shift: Use SCF=vshift=500 to artificially increase the energy of the virtual orbitals. This widens the HOMO-LUMO gap, reducing mixing between occupied and virtual orbitals and stabilizing the convergence process. The value can typically be reduced to 300 for less severe cases. This shift affects only the convergence path, not the final results [2].
• Fermi Smearing: Applying SCF=Fermi smears the electron occupation around the Fermi level, which is particularly helpful for metallic systems with a dense set of states near the Fermi energy [9] [2].
• Reduce Mixing Parameter: Using a smaller mixing parameter (e.g., 0.05 instead of the default 0.25) adds more damping, which can smooth out oscillations at the cost of slower convergence [11].

Step 4: Change the SCF Algorithm If the above steps fail, switch to a more robust algorithm.

• Quadratic Convergent SCF (QC-SCF): This method is robust but computationally expensive. It can be invoked with SCF=QC [2].
• MultiSecant Method: This is a modern and efficient alternative. As noted in the BAND documentation, it often succeeds where DIIS fails without increasing computational cost per iteration [11].

The Scientist's Toolkit: Research Reagent Solutions

The table below lists key "reagents"—computational techniques and parameters—used to troubleshoot SCF convergence, along with their primary function.

Research Reagent Solution	Primary Function in Troubleshooting
Energy Level Shift (SCF=vshift)	Increases HOMO-LUMO gap to prevent orbital mixing [2].
Fermi Smearing (SCF=Fermi)	Smears orbital occupancy for metallic/small-gap systems [2].
Quadratic Convergent SCF (SCF=QC)	Provides a robust, fallback algorithm when DIIS fails [9] [2].
MultiSecant Method	Modern alternative to DIIS for difficult convergence at similar cost [11].
Damping (Reduced Mixing)	Smoothens charge oscillations by reusing more of the old density [11].
Fine Integration Grid (int=ultrafine)	Ensures numerical accuracy, crucial for meta- and hybrid-functionals [2].
Alternative Initial Guess (guess=huckel, guess=core)	Provides a more stable starting point for the SCF procedure [2] [10].
2-amino-1-(1H-indol-3-yl)ethanol	2-amino-1-(1H-indol-3-yl)ethanol, CAS:46168-27-8, MF:C10H12N2O, MW:176.21 g/mol
1-(4-isopropylcyclohexyl)ethanol	1-(4-isopropylcyclohexyl)ethanol, CAS:63767-86-2, MF:C11H22O, MW:170.29 g/mol

MultiSecant vs. DIIS: A Comparative Analysis for Surface Systems

The choice of algorithm is pivotal for efficient SCF convergence in challenging systems. The following table provides a detailed comparison of the DIIS and MultiSecant methods.

Feature	DIIS (Direct Inversion in Iterative Subspace)	MultiSecant
Core Principle	Extrapolates a new Fock matrix by minimizing the residual error vector from previous iterations [9].	A quasi-Newton method that uses multiple previous steps to build an approximation to the Jacobian [11].
Computational Cost	Low per iteration.	Similar cost per iteration compared to DIIS [11].
Convergence Robustness	Can fail or show slow convergence for systems with small gaps due to charge sloshing [9].	Often more robust for difficult cases, such as metallic surfaces and large clusters [11].
Key Tunable Parameters	Subspace size (DIIS%Dimix), mixing parameter [11].	Can be used with minimal tweaking in most cases.
Recommended Use Case	Standard for small molecules and insulating systems with a good initial guess [9].	Preferred for metallic systems, surfaces, and cases where standard DIIS fails to converge [11].

FAQs on SCF Convergence Issues

Q: What are the first parameters to adjust when SCF convergence is slow or fails? A: For problematic systems, the primary approach is to use more conservative (smaller) mixing parameters. This stabilizes the SCF procedure. You can decrease the SCF%Mixing parameter and/or the DIIS%Dimix value [11]. Additionally, enabling the Degenerate option in the Convergence block is often beneficial for systems with nearly degenerate states [11].

Q: My geometry optimization does not converge, even though the SCF does. What accuracy settings should I check? A: When geometry optimization fails despite SCF convergence, the likely cause is insufficiently accurate gradients. To improve gradient accuracy, you should increase the number of radial points via the RadialDefaults block and set the NumericalQuality to Good or higher [11].

Q: Are there alternative algorithms if DIIS performs poorly? A: Yes, if the standard DIIS method is ineffective, two main alternatives are recommended. The MultiSecant method offers a different convergence approach at a similar computational cost per cycle [11]. Alternatively, the LIST method (specified via Diis Variant LISTi) can be tried, though it may increase the cost of individual SCF cycles [11].

Q: How can I manage convergence in difficult systems like slabs during a geometry optimization? A: For challenging geometry optimizations, you can use "automations" to dynamically adjust key parameters. It is often effective to start with a higher electronic temperature and looser SCF convergence criteria when geometry changes are large, and then progressively tighten these criteria as the optimization proceeds and gradients become smaller [11].

SCF Convergence Tolerances

The tables below summarize standard convergence tolerances for different levels of precision, as found in computational chemistry software. These values are crucial for quantifying convergence and ensuring the reliability of your results.

Table 1: Standard Convergence Tolerance Presets

Convergence Level	TolE (Energy)	TolRMSP (Density)	TolMaxP (Density)	TolErr (DIIS Error)
Loose	1e-5	1e-4	1e-3	5e-4
Medium	1e-6	1e-6	1e-5	1e-5
Strong	3e-7	1e-7	3e-6	3e-6
Tight	1e-8	5e-9	1e-7	5e-7
VeryTight	1e-9	1e-9	1e-8	1e-8
Extreme	1e-14	1e-14	1e-14	1e-14

Source: ORCA Manual, adapted from detailed threshold tables [3].

Table 2: Key Convergence Criteria and Descriptions

Criterion	Description	Typical Tight Value
TolE	Change in total energy between SCF cycles.	1e-8
TolRMSP	Root-mean-square change in the density matrix.	5e-9
TolMaxP	Maximum change in the density matrix.	1e-7
TolErr	The DIIS error vector, related to the commutation of Fock and density matrices [12].	5e-7
TolG	Norm of the orbital gradient.	1e-5

Source: ORCA Manual [3] and Q-Chem Manual [12].

Experimental Protocols for Convergence Testing

Protocol 1: Systematic Comparison of DIIS and MultiSecant Methods

• System Selection: Choose a set of benchmark systems relevant to your research, such as transition metal complexes or extended slab models.
• Baseline Calculation: Run a single-point energy calculation for each system using the default DIIS method and standard convergence criteria (e.g., Strong).
• MultiSecant Calculation: Run an identical calculation, but switch the SCF method to MultiSecant [11].
• Data Collection: For both calculations, record the (a) total number of SCF cycles to convergence, (b) final total energy, and (c) the evolution of the largest DIIS error or relevant residual in each cycle.
• Analysis: Compare the convergence rates and final energies between the two methods. A method that converges in fewer cycles is more efficient. Ensure the final energies are consistent.

Protocol 2: Assessing Stability with Tightened Tolerances

• Converge a System: Select a target molecule and converge it using TightSCF tolerances [3].
• Stability Analysis: Perform an SCF stability analysis on the converged wavefunction to check if it is a true local minimum or a saddle point [3].
• Re-converge from Perturbation: Slightly perturb the molecular geometry or the converged density and attempt to re-converge the SCF using both DIIS and MultiSecant methods.
• Result Interpretation: A robust method will consistently converge back to the same energy and electronic state despite the perturbation. Inconsistent convergence or convergence to a different state indicates sensitivity and a less reliable solution.

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Computational Parameters and Methods

Item	Function & Purpose	Relevant Input Key / Setting
DIIS Subspace Size	Controls the number of previous Fock matrices used for extrapolation. A larger subspace can improve convergence but uses more memory [12].	DIIS_SUBSPACE_SIZE (Q-Chem) [12]
SCF Mixing Parameter	Damps the updated Fock matrix between cycles. A smaller value is more conservative and stable for difficult cases [11].	SCF%Mixing (AMS/BAND) [11]
Electronic Temperature	Smears orbital occupations, which can help convergence in metallic systems or during initial geometry steps by preventing oscillations [11].	Convergence%ElectronicTemperature [11]
MultiSecant Algorithm	An alternative to DIIS for SCF convergence that can be more effective for some systems without increased cost per cycle [11].	SCF Method MultiSecant (AMS/BAND) [11]
Numerical Integration Grid	Defines the accuracy of numerical integrals for the exchange-correlation potential in DFT. A finer grid is crucial for accurate energies and gradients, especially with modern functionals [13].	NumericalQuality Good (AMS/BAND) [11]
Bisorcic	Bisorcic, CAS:39825-23-5, MF:C9H16N2O4, MW:216.23 g/mol	Chemical Reagent
(3-Hydroxyphenyl)phosphonic acid	(3-Hydroxyphenyl)phosphonic acid, CAS:33733-31-2, MF:C6H7O4P, MW:174.09 g/mol	Chemical Reagent

Workflow Diagram for SCF Convergence Troubleshooting

SCF Convergence Troubleshooting

Inside the Algorithms: How DIIS and MultiSecant Accelerate SCF Convergence

Core Concepts & FAQs

Frequently Asked Questions

• Q1: What is the fundamental principle behind Pulay's DIIS method? DIIS (Direct Inversion in the Iterative Subspace) is an extrapolation technique that accelerates convergence by constructing a new guess for the solution as a linear combination of approximate vectors from previous iterations. The coefficients for this linear combination are determined by minimizing the norm of a corresponding linear combination of error vectors, subject to the constraint that the coefficients sum to one [14]. This effectively minimizes the error in a least-squares sense within the constructed iterative subspace.

• Q2: What is the "commutator criterion" and how is it used as an error vector in electronic structure calculations? In the context of the Hartree-Fock or Kohn-Sham equations, the DIIS method often uses the commutator [F, P] between the Fock (or Kohn-Sham) matrix F and the density matrix P as the error vector. In a converged self-consistent field (SCF) solution, this commutator should be zero. Therefore, its norm serves as an excellent measure of the error for each iteration, guiding the DIIS algorithm toward the converged solution [14] [15].

• Q3: Why does my DIIS calculation sometimes diverge, especially at the start of a geometry optimization? DIIS is highly efficient close to a minimum but can struggle with poor initial guesses. The algorithm uses an approximation of the inverse Hessian matrix built from historical iteration data. If the initial steps are far from the solution, this information can be inaccurate and lead to divergence [16] [11]. This is particularly common in systems with complex electronic structures, such as metal slabs or molecules with distorted geometries.

• Q4: What is the key practical difference between the DIIS and MultiSecant methods for SCF convergence? The primary difference lies in their computational strategy and robustness. The DIIS method builds a subspace from previous iterations and can be sensitive to the initial guess and the POTIM parameter in VASP [16]. In contrast, the MultiSecant method (also known as the Limited-memory Broyden method) is a quasi-Newton approach that typically offers similar convergence acceleration per SCF cycle but is often more robust, sometimes converging systems where DIIS fails, and at no extra computational cost per iteration [11].

• Q5: How can I stabilize DIIS for a difficult-to-converge system like an iron slab? For problematic systems, more conservative SCF settings are recommended [11]:

  • Reduce the mixing parameter: Decrease the SCF%Mixing parameter (e.g., to 0.05).
  • Use a conservative DIIS strategy: Lower the DIIS%Dimix parameter (e.g., to 0.1).
  • Employ finite electronic temperature: Applying a small electronic temperature can smooth the energy landscape, making convergence easier, especially in the early stages of a geometry optimization when forces are large [11].

Troubleshooting Guide: Common DIIS Issues & Solutions

Problem	Symptom	Recommended Solution
SCF Oscillations	Total energy oscillates between values without converging.	- Decrease the mixing parameter (Mixing or SCF%Mixing) [11].- Use a smaller POTIM for ionic relaxation (IBRION=2 is more robust) [16].- Switch to the Conjugate Gradient algorithm (IBRION=2) if far from minimum [16].
Slow Convergence	Energy converges, but the number of iterations is very high.	- For VASP, use IBRION=1 (RMM-DIIS) which is faster near a minimum [16].- Ensure NELMIN is set to at least 4-8 for accurate forces in DIIS [16].- Consider using the LISTi DIIS variant (Diis%Variant LISTi) [11].
Divergence from Poor Initial Guess	SCF energy increases rapidly or fails immediately.	- Use a simpler initial guess (e.g., from a calculation with a smaller basis set) [11].- Apply damping or level-shifting techniques initially [15].- Use a finite electronic temperature at the start of a geometry optimization [11].
Linear Dependence in Basis	Calculation aborts with "dependent basis" error.	- Apply spatial confinement to diffuse basis functions [11].- Remove the most diffuse basis functions from the set.- Do not loosen the dependency criterion, as this compromises numerical accuracy [11].

Experimental Protocols & Methodologies

Protocol 1: Comparative Analysis of DIIS vs. MultiSecant for Surface Systems

Objective: To evaluate the convergence performance and computational cost of DIIS and MultiSecant algorithms for a transition metal surface system.

• System Setup: Construct a slab model of a pristine Pd(111) surface and an Fe(110) surface with a surface defect. Use the same k-point mesh and energy cutoffs for both.
• Initial Calculation: Perform a single-point energy calculation for each system using a minimal SZ basis to generate a stable initial density matrix.
• Algorithm Testing:
  • DIIS: Run the SCF calculation using the DIIS method with standard settings. Record the number of iterations, total time, and final energy.
  • MultiSecant: Restart from the initial density and run the SCF using the MultiSecant method. Record the same metrics.
• Parameter Sensitivity: Repeat step 3 for both algorithms, but introduce a 5% distortion to the atomic positions of the surface layer. Observe the change in convergence behavior.
• Analysis: Compare the number of SCF cycles, total CPU time, and convergence stability for both methods on the pristine and distorted systems [11].

Protocol 2: Automating Convergence for Complex Geometry Optimizations

Objective: To implement a robust, multi-stage geometry optimization for a molecule-on-slabsystem that automatically tightens convergence criteria as the geometry improves.

• Input Configuration: In the geometry optimization block, define engine automations that vary key parameters based on the optimization step or the maximum gradient.
• Initial Stage (Loose Settings):
  • Set a high initial electronic temperature (Convergence%ElectronicTemperature = 0.01) to aid initial SCF convergence.
  • Relax the SCF convergence criterion (Convergence%Criterion = 1.0e-3).
  • Limit the number of SCF steps per geometry iteration (SCF%Iterations = 30).
• Final Stage (Tight Settings):
  • Specify a lower final electronic temperature (Convergence%ElectronicTemperature = 0.001).
  • Tighten the SCF convergence criterion to the desired accuracy (Convergence%Criterion = 1.0e-6).
  • Allow more SCF iterations (SCF%Iterations = 300).
• Execution: Run the geometry optimization. The program will automatically interpolate parameter values between the defined initial and final states based on the optimization step number or the size of the gradients [11].

Essential Visualizations

DIIS Algorithm Workflow

MultiSecant vs. DIIS Convergence Profile

The Scientist's Toolkit: Key Research Reagents & Computational Parameters

Table: Essential Parameters for SCF Convergence Methods

Item/Parameter	Function/Description	Typical Value / Example
DIIS%Dimix	Controls the aggressiveness of the DIIS extrapolation. Lower values are more conservative and stable [11].	0.1 (conservative) to 0.5 (aggressive)
SCF%Mixing	The linear mixing parameter for the density or potential. Critical for stability in difficult systems [11].	0.05 (small, stable) to 0.2 (fast, risky)
POTIM	The time step or step size scaling for ionic motion. Affects the robustness of geometry optimization [16].	~0.5 (Can be optimized via trial steps in IBRION=2) [16]
Electronic Temperature (kT)	Smoothens orbital occupations, aiding SCF convergence in metallic systems or during initial optimization steps [11].	0.01 Ha (initial) -> 0.001 Ha (final)
Convergence%Criterion	The target accuracy for the SCF energy or density change. Can be automated during geometry optimization [11].	1e-3 (loose) -> 1e-6 (tight)
IBRION	VASP tag to select ionic relaxation algorithm. CG (2) is more robust, RMM-DIIS (1) is faster near minima [16].	1 (RMM-DIIS) or 2 (Conjugate Gradient)
MultiSecant Method	A robust quasi-Newton SCF convergence method that can be used as an alternative to DIIS [11].	SCF{ Method MultiSecant }
2,3-Dimethylpyrido[2,3-b]pyrazine	2,3-Dimethylpyrido[2,3-b]pyrazine, CAS:7154-32-7, MF:C9H9N3, MW:159.19 g/mol	Chemical Reagent
1,9-Nonanediol, dimethanesulfonate	1,9-Nonanediol, dimethanesulfonate, CAS:4248-77-5, MF:C11H24O6S2, MW:316.4 g/mol	Chemical Reagent

What is the MultiSecant method and how does it differ from DIIS?

The MultiSecant Method is a self-consistent field (SCF) convergence algorithm that serves as an alternative to the widely used Direct Inversion in the Iterative Subspace (DIIS). Both aim to accelerate the convergence of the SCF procedure, but they employ different mathematical strategies [11] [17].

The core principle of DIIS is to generate a new Fock matrix by making a linear combination of Fock matrices from previous iterations. The coefficients for this combination are determined by minimizing the error vector associated with the commutator SPF - FPS, which should be zero at convergence [18]. DIIS can be highly effective but sometimes has a tendency to "tunnel" through barriers in wave function space, potentially converging to a global rather than a local minimum [18].

In contrast, the MultiSecant method is a type of second-order quasi-Newton algorithm. These methods build an estimate of the inverse Hessian (or its action) using information from successive iterations to capture the curvature of the energy surface, which often leads to more robust convergence [11] [17]. It approximates the Newton-Raphson direction without the prohibitive cost of computing the exact Hessian, using secant conditions to iteratively update its approximation [17]. A key practical advantage is that the MultiSecant method typically incurs no extra cost per SCF cycle compared to the standard DIIS method [11].

The table below summarizes their key characteristics:

Feature	DIIS (Direct Inversion in Iterative Subspace)	MultiSecant Method
Core Principle	Minimizes error vector via linear combination of previous Fock matrices [18].	A quasi-Newton method using secant conditions to approximate the Hessian [11] [17].
Mathematical Basis	Linear algebra and error vector minimization.	Secant condition and iterative low-rank Hessian updates [17].
Computational Cost per Cycle	Low (depends on subspace size).	Similar to DIIS, with no significant extra cost per cycle [11].
Typical Performance	Fast for well-behaved systems, but can oscillate or diverge in difficult cases.	Often more stable and robust for problematic systems [11].

When should I consider switching from DIIS to the MultiSecant method?

You should consider using the MultiSecant method when your SCF calculations encounter persistent convergence problems, especially with systems that have complex electronic structures. The following scenarios are strong indicators for making the switch [11]:

• Standard DIIS Failures: When the standard DIIS procedure is unable to converge the SCF energy, often indicated by oscillating energy values or a consistently large error vector.
• Systems with Metallic or Near-Degenerate Character: Systems like metal slabs (e.g., Fe slabs), molecules with small HOMO-LUMO gaps, or those containing transition metals are often more difficult to converge and benefit from more conservative algorithms [11] [2].
• Complex Potential Energy Surfaces: When dealing with systems where the SCF solution might be unstable or when searching for specific local minima on a complex energy landscape [19].

How do I implement the MultiSecant method in my calculations?

Implementation is straightforward in quantum chemistry packages that support it. For instance, in the AMS/BAND code, you can activate the method with a simple input block [11]:

In many cases, no further tweaking is needed, as the method is designed to work efficiently out-of-the-box. The MultiSecantConfig block allows for advanced customization if required for particularly challenging cases [11].

What is a step-by-step workflow for troubleshooting SCF convergence?

The following diagram outlines a logical, step-by-step protocol for resolving SCF convergence issues, positioning the MultiSecant method within a broader strategy.

The Scientist's Toolkit: Research Reagent Solutions

This table details key "research reagents" – the computational tools and parameters – essential for implementing the advanced SCF convergence strategies discussed.

Tool/Solution	Function in Experiment	Example/Default Value
MultiSecant Algorithm	Provides a robust quasi-Newton SCF convergence pathway, often at no extra cost per cycle compared to DIIS [11].	SCF Method MultiSecant (AMS/BAND)
LIST/LISTi Algorithm	An alternative advanced algorithm that may converge when DIIS fails; can reduce the number of SCF cycles but increases cost per iteration [11].	Diis Variant LISTi (AMS/BAND)
Finite Electronic Temperature	Smears orbital occupations to increase the HOMO-LUMO gap, aiding initial convergence during geometry optimization [11].	Convergence ElectronicTemperature 0.01 (Hartree)
Energy Shift (VShift)	Increases the energy of virtual orbitals to prevent excessive mixing with occupied orbitals, stabilizing convergence [2].	SCF=VShift=400 (Gaussian)
Dependency Criterion (Bas)	Controls the threshold for detecting linear dependence in the basis set, which can cause numerical instability [11].	Bas 1e-8 (Tightened default)
Soft Confinement	Limits the diffuseness of basis functions, mitigating linear dependence issues, especially in slabs and bulk systems [11].	SoftConfinement Radius=10.0
Ethyltrioctylphosphonium bromide	Ethyltrioctylphosphonium Bromide|C26H56BrP	Get high-purity Ethyltrioctylphosphonium Bromide for your research. This phosphonium salt is for Research Use Only. Not for human or veterinary use.
Ethanethiol, 2-(trimethoxysilyl)-	Ethanethiol, 2-(trimethoxysilyl)-, CAS:7538-45-6, MF:C5H14O3SSi, MW:182.32 g/mol	Chemical Reagent

How do I validate a converged SCF solution is physically meaningful?

Convergence does not guarantee that the solution represents a true physical minimum on the electronic energy surface. A converged wave function could be unstable. SCF stability analysis is a critical post-convergence check [19] [3].

This analysis tests whether the solution is stable against small orbital rotations. If an instability is found, the wave function can be displaced along the direction of the unstable mode and used as a new initial guess for a further SCF calculation, a process that can be automated in some software to iteratively locate a stable minimum [19]. This is particularly important for open-shell systems and when studying diradicals or potential triplet states [19].

Frequently Asked Questions

1. What are the primary SCF convergence acceleration methods available in ADF, ORCA, and CP2K? The available methods vary by software. ADF offers methods like DIIS, LISTi, EDIIS, and the augmented Roothaan-Hall (ARH) method [4]. ORCA's default is a combination of DIIS and SOSCF, with the Trust Radius Augmented Hessian (TRAH) algorithm activating automatically if difficulties are detected [1]. CP2K's default is the MultiStepper method, but it also allows you to explicitly select DIIS or MultiSecant [7].

2. My SCF calculation for an open-shell transition metal complex in ORCA is oscillating wildly and will not converge. What is a robust strategy? For such pathological cases, a combination of strong damping, a larger DIIS subspace, and frequent rebuilds of the Fock matrix is often required. You can use the following settings as a starting point [1]:

3. How can I enforce stricter convergence criteria for a geometry optimization in ORCA to ensure high-quality results? Use the !TightOpt keyword for the geometry optimizer and the !TightSCF keyword (or equivalent block settings) for the SCF procedure. The TightSCF criteria are detailed in the table above [3]. To force the optimization to stop if the SCF does not fully converge, add SCFConvergenceForced to your input [1].

4. The SCF calculation in my ADF job is unstable. What DIIS parameters can I adjust for a more stable, slower convergence? For difficult systems in ADF, you can slow down the convergence to make it more stable by reducing the mixing parameters and increasing the number of DIIS vectors. A sample configuration is [4]:

Input Parameters and Code-Specific Blocks

SCF Convergence Tolerances in ORCA ORCA provides simple keywords that set a group of predefined tolerances. The TightSCF criteria are commonly used for demanding calculations on systems like transition metal complexes [3].

Criterion	LooseSCF	NormalSCF	StrongSCF	TightSCF
TolE (Energy Change)	1e-5	-	3e-7	1e-8
TolMaxP (Max Density Change)	1e-3	-	3e-6	1e-7
TolRMSP (RMS Density Change)	1e-4	-	1e-7	5e-9
TolErr (DIIS Error)	5e-4	-	3e-6	5e-7
TolG (Orbital Gradient)	1e-4	1e-3	2e-5	1e-5
DCAS.TolG	5.0e-3	1.0e-3	5.00e-4	2.5e-4

Code-Specific SCF Control Blocks

Software	Block / Section	Key Parameters	Purpose & Notes
ORCA [1] [3]	%scf ... end	MaxIter, DIISMaxEq, Shift, SOSCFStart	Controls the SCF procedure. DIISMaxEq (default 5) can be increased to 15-40 for difficult cases [1].
ADF [4]	SCF ... End	Mixing, N (in DIIS sub-block), Cyc	Mixing controls the fraction of the new Fock matrix; lower values (e.g., 0.015) stabilize difficult calculations [4].
BAND [7]	Convergence ... End	Criterion, Degenerate, ElectronicTemperature	Degenerate smoothens occupations near the Fermi level, which can aid convergence [7].
CP2K [20]	&SCF ... &END SCF	EPS_SCF, MAX_SCF, MIXING	EPS_SCF sets the convergence threshold, and MAX_SCF sets the maximum number of iterations [20].

The Scientist's Toolkit: Research Reagent Solutions

Item	Function in Computational Experiments
Trust Radius Augmented Hessian (TRAH)	A robust second-order SCF converger in ORCA for problematic systems; activates automatically when standard DIIS struggles [1].
SlowConv / VerySlowConv Keywords	ORCA keywords that apply damping to stabilize convergence in transition metal complexes and other difficult systems [1].
Periodic Pulay Method	A generalization of DIIS where Pulay extrapolation is performed periodically instead of every cycle, improving robustness for metallic and inhomogeneous systems [21].
Electronic Smearing	Techniques like Degenerate in BAND or ElectronicTemperature in CP2K that use fractional occupations to help converge systems with small HOMO-LUMO gaps [7] [4].
Initial Guess Strategies	Using MORead in ORCA to import orbitals from a previous, simpler calculation can provide a better starting point for the SCF [1].
iso-Decyl-acetate	iso-Decyl-acetate, CAS:69103-24-8, MF:C12H24O2, MW:200.32 g/mol
Diethyl 2-hydroxy-3-methylsuccinate	Diethyl 2-hydroxy-3-methylsuccinate, CAS:93504-92-8, MF:C9H16O5, MW:204.22 g/mol

Troubleshooting SCF Convergence: A Systematic Workflow

This diagram outlines a logical procedure for diagnosing and resolving SCF convergence issues.

FAQs: Troubleshooting SCF Convergence

• My calculation oscillates and never converges. What should I do? This is a classic sign that the SCF process is struggling to find a stable solution. Switching from DIIS to the MultiSecant method is often recommended as a first step, as it can handle these oscillations more effectively [7]. Additionally, you can try enabling fractional occupation number smoothing via the Degenerate key, which helps by slightly smearing occupations around the Fermi level, thus breaking degeneracies that cause oscillations [7].

• The SCF converges for my organic molecule but fails for my transition metal complex. Why? Transition metal complexes often have challenging electronic structures with near-degeneracies and open-shell characteristics [22]. In such cases, standard DIIS can be slow or fail entirely. Consider using MultiSecant or the more advanced MultiStepper method [7]. Research also suggests that alternative algorithms like QN-DIIS (a variant of DIIS) or machine learning-enhanced methods can show superior performance for metal complexes [23] [22].

• What does the "Criterion" for SCF convergence actually mean? The SCF convergence criterion is based on the self-consistent error, which measures the difference between the input and output density of an SCF cycle [7]. It is calculated as: ( \text{err} = \sqrt{\int dx \; (\rho\text{out}(x)-\rho\text{in}(x))^2 } ) The default value for this criterion is not a single number but depends on both the chosen NumericalQuality and the number of atoms in your system ( \sqrt{N_\text{atoms}} ) [7].

• When should I consider a hybrid approach? A hybrid approach is beneficial when a single method is not optimal throughout the entire SCF process. For instance, you might start with a robust method like MultiSecant to get close to the solution and then switch to the faster DIIS method for final convergence [23]. Some implementations also use Periodic Pulay, where DIIS extrapolation is performed at regular intervals instead of every cycle, which can improve robustness [24].

• What is "charge sloshing" and how can I fix it? Charge sloshing is a common convergence problem in metallic systems or large, flat molecules, characterized by slow oscillations of charge during the SCF cycle [24]. It is caused by the system's strong response to long-wavelength perturbations. To mitigate it, use a preconditioner like the Kerker preconditioner, which suppresses these problematic low-frequency modes [24].

The table below summarizes the core characteristics of the main SCF convergence algorithms.

Algorithm	Typical Use Case	Key Characteristics	Default in BAND
DIIS	Standard systems (normal organic molecules)	Fast convergence for well-behaved systems; can be prone to oscillation [23] [25].	No
MultiSecant	Problematic systems, oscillations	Robust alternative to DIIS; often helpful when DIIS fails [7].	No
MultiStepper	Default, general-purpose	A flexible and robust method that automatically adapts its strategy [7].	Yes

Performance Comparison Across Molecular Types

The performance of SCF algorithms can vary significantly depending on the chemical system. The following table summarizes findings from benchmark studies.

System Type	DIIS Performance	MultiSecant / Advanced Method Performance
Organic Molecules (at equilibrium)	Generally good and fast convergence [22].	Similar to DIIS for straightforward cases [22].
Organic Molecules (near transition state)	Can struggle with convergence [22].	More robust convergence observed [22].
Transition Metal Complexes	Often slow or fails to converge [23] [22].	QN-DIIS and r-GDIIS show superior, more robust convergence [23] [22].

Experimental Protocol: A Step-by-Step Workflow for Troubleshooting

Follow this structured protocol to diagnose and resolve SCF convergence issues.

• Initial Setup & Baseline Run

  • Start with the default settings (often Method=MultiStepper in BAND) [7].
  • Ensure your geometry is reasonable and your basis set is appropriate.
  • Run the calculation and note the convergence behavior.

• Diagnosis and Initial Actions

  • Symptom: Slow, steady progress but not converging within the iteration limit.
    • Action: Increase the SCF Iterations limit [7].
  • Symptom: Large oscillations in the SCF error.
    • Action 1: Switch the method to Method=MultiSecant [7].
    • Action 2: Enable electronic smearing by setting Convergence Degenerate to default or a specific energy width [7].
  • Symptom: Calculation is stuck early on (e.g., in a metallic system).
    • Action: Implement a preconditioner like Kerker to suppress "charge sloshing" [24].

• Advanced Troubleshooting

  • If oscillations persist with MultiSecant, consider reducing the Mixing parameter to dampen the updates [7].
  • For transition metal complexes or severely problematic cases, consult your software's documentation for advanced methods like r-GDIIS (a reset-enabled DIIS) or machine learning-based optimizers like S-GEK/RVO [22].
  • As a last resort, break spatial or spin symmetry in your initial guess using keys like SpinFlip or StartWithMaxSpin to guide the calculation towards the desired state [7].

SCF Algorithm Selection Workflow

The diagram below outlines the logical decision process for selecting an SCF algorithm.

The Scientist's Toolkit: Key SCF Parameters and Materials

This table details the essential "research reagents" – the key input parameters and concepts – for controlling SCF convergence.

Item / Parameter	Function / Explanation
SCF Method	The core algorithm (DIIS, MultiSecant, MultiStepper) used to converge the density [7].
Convergence Criterion	The error tolerance that defines when the SCF cycle is stopped [7].
Mixing Parameter	The damping factor for updating the potential/density. A lower value stabilizes oscillation but can slow convergence [7].
Degenerate Key	Smears orbital occupations near the Fermi level, helping to resolve near-degeneracies that hinder convergence [7].
Preconditioner	A mathematical operator that transforms the problem to improve the conditioning of the SCF equations, crucial for metals [24].
SpinFlip	Used to break initial spin symmetry, essential for converging different magnetic states (e.g., antiferromagnetic) [7].

Advanced Troubleshooting: Taming Difficult SCF Convergence in Biomedical Systems

Frequently Asked Questions

Q1: My SCF calculation for a metallic slab is oscillating and will not converge. What should I adjust? This is a classic sign of "charge sloshing," common in metallic or inhomogeneous systems. The default DIIS method can sometimes stagnate for these cases. First, try switching from DIIS to the MultiSecant method, which often handles such systems more robustly without extra cost per cycle [11]. Alternatively, implement a more conservative mixing strategy by simultaneously reducing the SCF%Mixing parameter to 0.05 and the DIIS%DiMix parameter to 0.1 [11]. For plane-wave codes, using Kerker damping (e.g., METHOD KERKER_MIXING) can specifically suppress long-range charge oscillations [26] [27].

Q2: The SCF converges for a simple molecule but diverges during a geometry optimization of a large system. How can I stabilize it? Geometry optimizations place varying demands on the SCF procedure. Use automations to dynamically adjust SCF parameters based on the optimization step. For instance, you can start with a looser SCF convergence criterion and a higher electronic temperature to smooth initial convergence, then tighten them as the geometry approaches its minimum [11].

Q3: My calculation was going well but then the DIIS error became huge and the program reset the subspace. What happened? As the Fock matrix nears self-consistency, the linear equations solved by DIIS can become severely ill-conditioned, which triggers an automatic reset of the DIIS subspace [12]. This is a built-in safety feature. To prevent this, you can reduce the size of the DIIS subspace (DIIS_SUBSPACE_SIZE) to limit the number of previous Fock matrices used, which improves the conditioning of the problem [12]. Additionally, for the related MultiSecant method, increasing the REGULARIZATION parameter can help stabilize the matrix inversion [26] [27].

Q4: Are there any simple changes that can help with difficult SCF convergence? Yes, several straightforward checks can help:

• Enable smearing: Setting Convergence%Degenerate Default slightly smears occupations around the Fermi level, which can greatly improve convergence in systems with near-degeneracies [11].
• Check precision: Ensure your numerical integration grid and density fitting quality are sufficient. Convergence problems can be caused by inadequate precision [11].
• Use a better initial guess: If available, use a guess derived from atomic orbitals (InitialDensity psi) or restart from a calculation with a smaller basis set [7] [11].

Troubleshooting Guides

Guide 1: Diagnosing and Remedying SCF Oscillations and Divergence

Observation	Likely Cause	Recommended Action
Large, regular energy fluctuations in early SCF cycles	Insufficient initial damping	Activate damping (e.g., SCF_ALGORITHM = DP_DIIS) for the first few cycles [28].
Divergence in metallic/metallic-like systems	Charge sloshing	Switch from DIIS to MultiSecant method [11] or activate Kerker preconditioning [26] [27].
DIIS works then suddenly fails with large error	Ill-conditioned DIIS matrix	Reduce DIIS subspace size [12] or impose a regularization parameter [26] [27].
Slow convergence in all systems	Overly conservative mixing	For Pulay/DIIS, ensure an adequate number of previous steps are stored (NBUFFER) [26] [27].

Guide 2: Systematic Protocol for Tuning SCF Parameters

This protocol provides a step-by-step methodology for achieving SCF convergence in challenging systems, framed within the context of MultiSecant vs. DIIS research.

1. Initial System Assessment and Baseline

• Objective: Establish a stable, conservative starting point.
• Protocol:
  • Start with a simple density mixing method (METHOD DIRECT_P_MIXING) or linear mixing with a low mixing parameter (ALPHA 0.1) [26] [27].
  • Use a low DIIS%DiMix (e.g., 0.1) if DIIS is enabled [11].
  • Enable slight electronic smearing (Convergence%Degenerate Default) [11].
  • Run for a limited number of cycles (e.g., 20-30) to diagnose the behavior of the unconverged system.

2. Convergence Accelerator Selection and Tuning

• Objective: Apply an efficient convergence accelerator based on system characteristics.
• Protocol:
  • For molecules and homogeneous solids: Begin with standard DIIS. Use a subspace size of 8-15. If the calculation stagnates, try the Periodic Pulay method, which applies DIIS extrapolation only every few iterations with linear mixing in between, often improving robustness [21].
  • For metals, slabs, and inhomogeneous systems: Start directly with the MultiSecant method (SCF%Method MultiSecant) [7] [11]. This method is often more robust for these systems.
  • Key Tuning Parameters:
    • DIIS: DIIS_SUBSPACE_SIZE (size), DIIS%DiMix (aggression) [12] [7].
    • MultiSecant/Pulay: NBUFFER (history length), ALPHA/BETA (mixing), REGULARIZATION (stability) [26] [27].

3. Advanced Stabilization Techniques

• Objective: Overcome persistent divergence.
• Protocol:
  • Employ Damping: Use a dedicated damping algorithm (e.g., SCF_ALGORITHM = DP_DIIS) for the first 5-10 cycles with a moderate damping parameter (NDAMP 50-75) [28].
  • Use Kerker Preconditioning: In plane-wave codes, for metals, set METHOD KERKER_MIXING. Tune the BETA parameter to control the damping of long-wavelength modes [26] [27].
  • Dynamic Workflows: For geometry optimizations, implement engine automations to relax SCF criteria in the early stages and tighten them as the structure converges [11].

Experimental Protocols for Method Comparison

When conducting research on SCF convergence for "surface systems," a rigorous experimental protocol is required to compare DIIS, MultiSecant, and their variants fairly.

1. Benchmarking System Selection

• Select a diverse set of benchmark systems that are representative of your research focus on surfaces [21]:
  • Metallic surfaces: e.g., Pd or Fe slab [11].
  • Insulating surfaces: e.g., a cleaved oxide slab.
  • Adsorbate-covered surfaces: A molecule adsorbed on a metal slab, which introduces inhomogeneity.

2. Controlled Performance Metrics

• For each system and parameter set, measure the following quantitative metrics [7] [21]:
  • Number of SCF iterations to convergence.
  • Total CPU time (or wall time).
  • Robustness: Record the success rate out of multiple trials from different initial guesses.
  • Energy trajectory: Monitor the convergence of the total energy, log(ΔE) vs. iteration, to identify oscillations or stagnation.

3. Parameter Sensitivity Analysis

• For each method (DIIS, MultiSecant), test the sensitivity to its key parameters while keeping all other computational settings identical. The table below summarizes the core parameters to investigate, synthesized from multiple software manuals.

Table 1: Key Parameters for SCF Convergence Methods

Method	Core Tuning Parameters	Function & Recommended Investigation Range
DIIS	DIIS_SUBSPACE_SIZE	History length. Test 5-20 [12].
	DIIS%DiMix / MIXING	Aggression of extrapolation. Test 0.05 - 0.2 [7] [11].
MultiSecant / Pulay	NBUFFER	History length. Test 4-10 [26] [27].
	ALPHA / PULAY_BETA	Linear mixing parameter. Test 0.1 - 0.4 [26] [27].
	REGULARIZATION	Stabilizes matrix inversion. Test 1e-5 to 1e-7 [26] [27].
Damping	NDAMP (ALPHA)	Damping factor (0-100). 75 is a common default [28].
	MAX_DP_CYCLES	Iterations with damping active. Test 3-20 [28].
Kerker	BETA	Denominator for charge sloshing. ~0.5 Bohr⁻¹ default [26] [27].

SCF Convergence Optimization Workflow

The following diagram maps the logical decision process for optimizing SCF convergence, integrating the methods and parameters discussed above.

The Scientist's Toolkit: Research Reagent Solutions

In computational chemistry, the "research reagents" are the key parameters and algorithmic choices that define the numerical experiment.

Table 2: Essential Computational Reagents for SCF Convergence Studies

Reagent (Parameter/Algorithm)	Function in the "Experiment"	Typical Concentration (Default Value)
DIIS	Convergence accelerator; extrapolates using error vectors from previous steps [12].	DIIS_SUBSPACE_SIZE = 15 [12]
MultiSecant	Convergence accelerator; a variant of Pulay/DIIS that can be more robust for complex systems [7] [11].	NBUFFER = 4 [26] [27]
Mixing Parameter (ALPHA)	The fraction of new density/potential mixed into the old for simple damping [26] [28].	0.4 [26] [27]
Damping (NDAMP)	Stabilizes early SCF cycles by mixing consecutive density matrices [28].	75 [28]
Kerker BETA	Preconditioner that dampens long-wavelength (low-freq.) density changes to suppress "charge sloshing" [26] [27].	0.5 bohr⁻¹ [26] [27]
Electronic Temperature	Smears electronic occupations around the Fermi level, aiding convergence in metallic/small-gap systems [7] [11].	0.0 Ha (default) [7]

Frequently Asked Questions (FAQs) on SCF Convergence

Q1: What are the initial steps I should take if my SCF calculation fails to converge? For problematic cases, the first course of action is to adopt more conservative settings. This typically involves reducing the mixing parameter (SCF%Mixing) and/or the DIIS-specific mixing parameter (DIIS%DiMix). Using a smaller basis set (e.g., SZ) for an initial calculation to generate a better starting density for a subsequent restart with the target basis set can also be highly effective [11].

Q2: When should I consider alternatives to the standard DIIS method? If DIIS stagnates or performs poorly, which is sometimes observed in metallic or inhomogeneous systems, you should consider switching to other algorithms. The MultiSecant method is a highly recommended alternative, as it comes at no extra cost per SCF cycle compared to DIIS. The LIST method is another option, which may increase the cost per iteration but can reduce the total number of SCF cycles [11] [21].

Q3: How can electron smearing help with convergence, and what are its trade-offs? Applying a finite electronic temperature (smearing) smooths occupation numbers around the Fermi level, which can significantly improve convergence in systems with metallic character or near-degeneracies at the Fermi level [11] [7]. The trade-off is that the calculated energy deviates from the true ground state energy. For geometry optimizations, a practical strategy is to use a higher electronic temperature during initial steps (when forces are large) and progressively reduce it as the geometry converges [11].

Q4: My calculation fails with a "dependent basis" error. What does this mean and how can I fix it? This error indicates that the Bloch basis set constructed from your atomic orbitals is nearly linearly dependent at some k-points, threatening numerical accuracy. The recommended solution is not to loosen the dependency criterion but to adjust the basis set itself. Using confinement to reduce the range of diffuse basis functions, particularly for atoms in the bulk of a material, is an effective way to resolve this issue [11].

Troubleshooting Guide: A Structured Approach to SCF Problems

Step 1: Initial Diagnosis and Conservative Settings

Begin by verifying general accuracy settings. Insufficient precision in numerical integration (controlled by NumericalQuality) or using too few k-points can be the root cause of convergence problems [11].

• Action: Increase NumericalQuality and ensure k-space sampling is adequate.
• Action: Implement conservative mixing parameters.
  Source: [11]

Step 2: Algorithm Switching and Advanced Mixing

If the above steps fail, the core SCF convergence algorithm itself should be changed.

• Action: Switch from DIIS to the MultiSecant method.
  Source: [11]
• Action: Consider the Periodic Pulay method, a generalization of DIIS. Research has shown that performing Pulay (DIIS) extrapolation only once every few SCF cycles, with linear mixing in between, can improve both the efficiency and robustness of convergence across a wide range of materials [21].

Step 3: Leveraging Electron Smearing for Stubborn Cases

For the most difficult cases, using a finite electronic temperature is a powerful fallback strategy.

• Action: Enable smearing to handle near-degeneracies. The Degenerate key smoothens occupations automatically if convergence is problematic, but you can also set it manually [7].

• Action: For geometry optimizations, use automations to vary the electronic temperature and SCF convergence criteria throughout the process. This ensures stability in the beginning and accuracy at the end [11].
  Source: [11]

The following workflow diagram summarizes the decision process for applying these strategies:

Quantitative Data and Method Comparison

Table 1: Comparison of SCF Convergence Acceleration Methods

Method	Key Principle	Typical Use Case	Advantages	Considerations
DIIS (Pulay) [12] [21]	Minimizes error vector from commutator [S,P,F] using previous Fock matrices.	Standard for most well-behaved systems (insulators, molecules).	Simple, fast, widely implemented and understood.	Can stagnate in metals/inhomogeneous systems; may converge to wrong state.
MultiSecant [11]	Multi-secant type method related to Broyden/Quasi-Newton approaches.	General alternative to DIIS, especially if DIIS performs poorly.	No extra cost per cycle vs DIIS; often more robust.	Default in some modern codes (AMS/BAND).
Periodic Pulay [21]	Applies Pulay extrapolation periodically, with linear mixing in between.	Metallic, inhomogeneous, or other systems where standard DIIS fails.	Improved robustness & efficiency over DIIS; simple to implement.	Requires choosing an interval for Pulay steps.
LIST [11]	Variant of DIIS method.	Problematic cases where standard DIIS fails.	Can reduce total number of SCF cycles.	Higher computational cost per SCF iteration.

Table 2: Electron Smearing Parameters for Convergence

Parameter / Keyword	Function	Default Value (Typical)	Recommended Troubleshooting Value
Convergence%ElectronicTemperature [11] [7]	Smears occupations with a finite temperature (kT in Hartree).	0.0	0.001 - 0.01 (for initial convergence)
Convergence%Degenerate [7]	Automatically smoothens occupations around Fermi level if convergence is slow.	Default (internal logic)	Default (ensure it's not disabled)
Convergence%NoDegenerate [7]	Disables automatic occupation smoothing.	No	No (keep disabled to allow smearing)
SCF%Mixing [11] [7]	Damping parameter for updating potential/density.	0.075	Reduce to 0.05 or lower

The Scientist's Toolkit: Essential Research Reagents & Computational Materials

Table 3: Key Computational Materials and Their Functions

Material / Computational "Reagent"	Function in the Study of SCF Convergence	Example Context from Literature
Transition Metal Surfaces & Alloys [29]	Prototypical challenging systems for SCF convergence due to complex, localized d-electron states.	Used to test and develop new chemisorption models and convergence strategies.
Charge Density Wave (CDW) Materials (e.g., TXâ‚‚, T=Ti,Nb,Ta; X=Se,S) [30]	Model systems for testing finite-temperature smearing methods and their effect on predicting phase transitions.	Fermi smearing used to simulate electronic excitation effects on phonon softening.
Pd and Fe Slabs [11]	Benchmark systems of varying convergence difficulty (Pd = easier, Fe = more difficult).	Cited as examples for determining the need for conservative SCF settings.

Troubleshooting Guide: Frequently Asked Questions (FAQs)

Q1: My self-consistent field (SCF) calculations oscillate and fail to converge, especially for metallic or inhomogeneous systems. Is DIIS the problem, and what are the alternatives?

Pulay's Direct Inversion in the Iterative Subspace (DIIS) is the most widely used method for accelerating SCF convergence. However, it can stagnate or perform poorly for certain metallic and inhomogeneous systems [21]. This behavior is often a sign of charge sloshing, where the electron density oscillates between iterations instead of settling to a solution.

• Solution 1: The Periodic Pulay Method: This is a robust alternative that combines the benefits of linear mixing and DIIS. Instead of performing a Pulay extrapolation every SCF cycle, it is applied only at periodic intervals (e.g., every 4th or 5th iteration), with linear mixing used in between [21]. This simple modification can significantly improve both the efficiency and robustness of convergence compared to standard DIIS [21].
• Solution 2: ADIIS+DIIS Combination: The Augmented DIIS (ADIIS) method uses the augmented Roothaan-Hall energy function to determine the DIIS coefficients, making it more robust. For challenging cases, a combination of ADIIS and traditional DIIS ("ADIIS+DIIS") has proven highly reliable and efficient [31].
• Solution 3: Method Switching: Some codes allow for initial DIIS iterations followed by a switch to a more stable, direct minimization algorithm to converge difficult cases to the true minimum [12].

Q2: In my calculations on ion-water clusters, the many-body expansion (MBE) energies show wild oscillations and diverge as the system grows. What is the cause?

This is a classic symptom of delocalization error (a form of self-interaction error) poisoning density-functional theory (DFT) when used with a many-body expansion [32]. The error creates a feedback loop leading to runaway error accumulation, which is minor in small water clusters but becomes catastrophic in moderately larger ones like F⁻(H₂O)₁₅ [32].

• Mitigation Strategies:
  • Functional Choice: Semilocal functionals (GGAs) show severe divergence. Hybrid functionals can help, but only if the fraction of exact exchange is 50% or more. Meta-GGAs like ωB97X-V and SCAN are insufficient to eliminate the divergent behavior [32].
  • Energy-Based Screening: Culling unimportant subsystems in the expansion can successfully forestall divergent behavior [32].
  • Wavefunction Methods: Using Hartree-Fock theory for the MBE does not exhibit this divergent behavior, as it is free from self-interaction error [32].

Q3: My open-shell calculations show high spin contamination (<Ŝ²> deviates significantly from the ideal value). Are my results reliable?

Spin contamination occurs when an unrestricted wavefunction is not an eigenfunction of the total spin operator <Ŝ²>, leading to an artificial mixture of spin states. This can cause errors in geometries, energies, and population analyses [33].

• Diagnosis: Compare the computed <Ŝ²> value to its ideal quantum value, s(s+1), where s is half the number of unpaired electrons (e.g., 0.75 for a doublet, 2.0 for a triplet). A deviation of more than 10% is often a cause for concern [33].
• Solutions:
  • Restricted Open-Shell (ROHF) Calculations: This method uses a single set of orbitals, preventing spin contamination but at a higher computational cost and with potential loss of spin polarization data [33].
  • Functional Selection: Pure DFT functionals typically exhibit less severe spin contamination than hybrid functionals. The spin contamination increases with the percentage of exact Hartree-Fock exchange in a functional [33].
  • Spin-Adapted Methods: For specific methods like Spin-Flip TDDFT, spin contamination is inherent. In such cases, using a spin-adapted (SA-) variant can provide spin-pure states, though this may come with limitations (e.g., no available geometry optimization routines) [34].
  • Technical Checks: In unrestricted calculations, ensure that the DIIS procedure correctly handles the alpha and beta error vectors. If they cancel each other out, it can mask a false convergence; setting DIIS_SEPARATE_ERRVEC = TRUE can help diagnose this [12].

Experimental Protocols & Methodologies

Protocol: Diagnosing and Remedying SCF Oscillations with Periodic Pulay

Objective: To achieve robust SCF convergence for systems where standard DIIS fails.

Materials/Software: An electronic structure code with the capability to modify the DIIS frequency (e.g., an implementation of the Periodic Pulay method) [21].

Procedure:

• Initial Setup: Begin a standard SCF calculation using DIIS.
• Identify Failure: Note the oscillation or stagnation of the total energy or density residual.
• Implement Periodic Pulay: Switch to a Periodic Pulay scheme. A typical effective parameter is to perform one Pulay extrapolation every four SCF iterations.
• Linear Mixing: On the non-Pulay iterations, use a simple linear mixing scheme for the electron density or density matrix.
• Convergence Monitoring: Continue the SCF procedure until the desired convergence threshold (e.g., energy change below 10⁻⁵ au) is reached.

Logical Workflow:

Protocol: Assessing Spin Contamination in Open-Shell Systems

Objective: To evaluate the reliability of an open-shell calculation by measuring spin contamination and to apply corrective methods.

Materials/Software: A quantum chemistry package (e.g., Q-Chem, Gaussian) capable of performing unrestricted calculations and reporting the <Ŝ²> expectation value [33] [34].

Procedure:

• Run Unrestricted Calculation: Perform a single-point energy or geometry optimization using an unrestricted method (e.g., UDFT, UHF).
• Check Output: Locate the computed <Ŝ²> value in the output file.
• Calculate Ideal Value: Compute the ideal value, s(s+1). For a system with one unpaired electron (doublet), the ideal value is 0.75.
• Evaluate Deviation: If the deviation is large (e.g., >10%), the results may be unreliable.
• Remedial Actions:
  • Switch to ROHF/RODFT: Restart the calculation using a restricted open-shell method.
  • Adjust Functional: If using a hybrid functional, try a pure DFT functional with less exact exchange.
  • Use Advanced Methods: For Spin-Flip TDDFT, consider spin-adapted variants if available, acknowledging their limitations [34].

The Scientist's Toolkit: Research Reagent Solutions

Table 1: Key Computational Tools for Addressing SCF Failure Modes

Tool / Method	Primary Function	Application Context
Periodic Pulay [21]	SCF convergence acceleration	Robust alternative to DIIS for metallic/inhomogeneous systems and charge sloshing.
ADIIS (Augmented DIIS) [31]	SCF convergence acceleration	Uses an energy-based minimization for DIIS coefficients; often used in combination with DIIS.
DIIS (Direct Inversion in Iterative Subspace) [12]	SCF convergence acceleration	Standard method; can fail for specific systems but excellent for most.
Restricted Open-Shell (ROHF/RODFT) [33]	Open-shell calculation	Eliminates spin contamination by enforcing a restricted orbital set.
Hybrid Density Functionals [32] [33]	Electron exchange-correlation	Higher exact exchange (>50%) can mitigate delocalization error but may worsen spin contamination.
Energy-Based Screening [32]	Many-body expansion stability	Culls unimportant subsystems in MBE to prevent divergence caused by delocalization error.
Spin-Adapted SF-TDDFT [34]	Excited state calculation	Provides spin-pure states for spin-flip methods, though may lack analytical gradients.

Table 2: Quantitative Data on Delocalization Error in DFT-based Many-Body Expansion

Parameter	Value / Observation	Context / Implication
Critical Cluster Size	N ≳ 15 water molecules around F⁻ [32]	Delocalization error becomes catastrophic in moderately large ion-water clusters.
PBE n-body Contributions	n=4: -115.9 kcal/mol (F⁻ terms); n=5: +193.0 kcal/mol (F⁻ terms) [32]	Wild oscillations in the sign and magnitude of many-body terms lead to divergence.
HF n-body Contributions	n=4: -0.6 kcal/mol (water terms); n=5: +0.1 kcal/mol (water terms) [32]	Wavefunction methods like HF are free from this error and show convergent behavior.
Required Exact Exchange	≳50% [32]	The fraction of exact exchange in a hybrid functional needed to counteract divergent behavior.
Error Suppression Factor	1.56(4)-fold reduction [35] [36]	Achieved by increasing the color code distance in quantum error correction, an analogous scaling concept.

Frequently Asked Questions (FAQs)

Q1: Why does my self-consistent field (SCF) calculation for a transition metal surface stagnate or fail to converge?

SCF convergence challenges in metallic and inhomogeneous systems often arise from the complex electronic structure of transition metals, which can cause standard algorithms like Pulay's Direct Inversion in the Iterative Subspace (DIIS) to perform poorly [21]. The DIIS method can struggle with the slow charge sloshing and extended energy landscapes common in periodic surface calculations. Employing a method like Periodic Pulay, which alternates Pulay extrapolation with linear mixing, can significantly improve robustness [21].

Q2: What is the most accurate method for calculating adsorption energies on transition metal surfaces?

For high accuracy, a combined approach is often best. While standard Generalized Gradient Approximation (GGA) functionals like PBE are common, they can struggle with a balanced description of covalent and non-covalent interactions [37]. For improved accuracy, consider:

• Hybrid functionals: Offer higher accuracy but at a greatly increased computational cost, making them prohibitive for large, extended systems [37].
• Corrective cluster schemes: A promising approach involves applying a higher-level correction (e.g., from CCSD(T) calculations) to a small, representative metal cluster to improve the periodic band structure adsorption energy. This method has shown mean absolute errors as low as 2.2 kcal mol⁻¹ for adsorption energies [37].

Q3: How can I accurately predict the surface energy of an irregularly shaped metal nanoparticle?

Surface energy is a critical stability descriptor for nanocatalysts. For non-uniform structures, traditional methods based on slab models are insufficient. A modern approach uses machine learning:

• Features: A model can be trained using easy-to-compute geometric features, such as the coordination number (CN) of surface atoms [38].
• Performance: A neural network model using these features has been shown to predict surface energies for various morphologies with a mean absolute error of 0.091 J m⁻² [38].

Troubleshooting Guides

Issue: Slow or Unstable SCF Convergence for Metallic Slabs

Problem: The SCF iteration oscillates or fails to converge when calculating the electronic structure of a transition metal surface.

Solution: Implement the Periodic Pulay method [21].

• Method: Instead of applying Pulay (DIIS) extrapolation at every SCF cycle, perform it only once every few iterations (e.g., every 4th or 5th iteration).
• Intermediate Steps: Use simple linear mixing for the iterations between Pulay steps.
• Rationale: This approach reduces the chance of DIIS extrapolating from poor-quality, non-linear density inputs, which is a common cause of instability in metallic systems.
• Implementation: This is a generalization of standard DIIS and can be easily incorporated into electronic structure codes that already use Pulay mixing.

Issue: Inaccurate Adsorption Energy for a Molecular Adsorbate

Problem: Standard DFT functionals yield poor adsorption energies, either overestimating chemisorption or underestimating physisorption.

Solution: Adopt a multi-level quantum mechanics approach [37].

• Perform a Periodic DFT Calculation: First, compute the adsorption energy on your extended surface model using a functional like BEEF-vdW, which offers a reasonable balance [37].
• Model the Local Site with a Cluster: Create a small cluster of metal atoms that represents the local adsorption site (e.g., a 3-10 atom cluster).
• Compute a High-Level Correction: Calculate the adsorption energy on this small cluster using a highly accurate (but computationally expensive) method like CCSD(T).
• Apply the Correction: The correction is derived from the difference between the high-level and DFT-level energies on the cluster. This value is then used to improve the periodic DFT adsorption energy, effectively transferring the accuracy of the quantum chemical method to the extended system.

Research Reagent Solutions: Computational Tools Table

The following table summarizes key computational "reagents" and their functions in modeling transition metal surfaces.

Research Reagent	Function & Purpose	Key Consideration
BEEF-vdW Functional [37]	A dispersion-corrected GGA functional for calculating adsorption energies. Provides a balanced description for many chemisorbed systems.	Can yield errors for physisorbed systems; space for improvement remains [37].
Periodic Pulay Method [21]	An SCF convergence accelerator. Improves robustness and efficiency for metallic and inhomogeneous systems.	More robust than standard DIIS for difficult systems like metal surfaces [21].
Machine Learning (ML) Model [38]	Predicts surface energy of nanostructures and clusters using geometric descriptors.	Uses coordination number as an input feature; achieves high accuracy (MAE 0.091 J m⁻²) [38].
Cluster Correction Scheme [37]	Improves periodic DFT adsorption energies via higher-level calculations on small clusters.	Corrects for limitations of standard functionals; can achieve chemical accuracy (~1-2 kcal/mol) [37].
Tiling Scheme [38]	Measures the surface area of irregular nanoparticles and defective surfaces atomistically.	More accurate for nanostructures than simple cell-axis projection [38].

Experimental Protocol: Combining Periodic DFT with Cluster Corrections for Accurate Adsorption Energies

Aim: To calculate an accurate adsorption energy for an adsorbate on a transition metal surface, targeting errors below 3 kcal/mol [37].

Procedure:

• Periodic Calculation:
  • Build a periodic slab model of the relevant transition metal surface (e.g., Pt(111), Ni(111)).
  • Optimize the geometry of the clean slab and the adsorbate-surface system using a GGA functional like PBE or RPBE.
  • Compute the adsorption energy: ( E{\text{ads, periodic}}^{\text{DFT}} = E{\text{adsorbate@surface}} - E{\text{surface}} - E{\text{adsorbate}} )

• Cluster Model Calculation:

  • Construct a small metal cluster (e.g., ( M_6 )) that mimics the local coordination environment of the adsorption site.
  • Perform a single-point energy calculation for the adsorbate bound to the cluster at the DFT level (using the same functional as step 1).
  • Perform a single-point energy calculation for the same configuration using a high-level method (e.g., CCSD(T)).
  • Compute the cluster correction: ( \Delta E{\text{cluster}} = E{\text{ads, cluster}}^{\text{High-Level}} - E_{\text{ads, cluster}}^{\text{DFT}} )

• Final Energy Calculation:

  • Apply the cluster correction to the periodic adsorption energy to obtain the final, improved value:
  • ( E{\text{ads, final}} = E{\text{ads, periodic}}^{\text{DFT}} + \Delta E_{\text{cluster}} )

Workflow Diagram:

Experimental Protocol: Implementing the Periodic Pulay Method

Aim: To achieve robust and efficient SCF convergence for a transition metal surface calculation.

Procedure:

• Initialization: Begin the SCF cycle as usual with an initial guess for the electron density.
• Set Mixing Parameters: Define two key parameters:
  • PULAY_INTERVAL (N): The interval (number of iterations) at which Pulay extrapolation is performed (e.g., N=4).
  • MIXING_PARAMETER (α): The linear mixing parameter used for non-Pulay iterations (e.g., α=0.1).
• SCF Iteration Loop:
  • For SCF iterations that are not multiples of PULAY_INTERVAL, generate the new Fock matrix and density using linear mixing: ( \rho{n+1} = (1 - \alpha) \rhon + \alpha \rho_{\text{output}} )
  • For SCF iterations that are multiples of PULAY_INTERVAL, generate the new Fock matrix using Pulay extrapolation (DIIS) from the history of the previous N iterations.
• Convergence Check: Check for convergence after each step. Repeat the loop until the desired convergence criteria are met.

Workflow Diagram:

Benchmarking Performance: A Direct Comparison of DIIS and MultiSecant Efficacy

Frequently Asked Questions

Q1: What are the primary causes of SCF convergence failure in metallic and large-scale systems?

The main cause is charge sloshing, which refers to long-wavelength charge oscillations that are difficult to dampen, particularly in metallic systems with very small HOMO-LUMO gaps [9]. The DIIS method, while excellent for small molecules and insulators, often struggles with this phenomenon. The inherent linearity assumption in DIIS becomes less valid in these problematic cases, leading to slow convergence or complete failure [9].

Q2: How can I improve SCF convergence for a difficult metallic system?

You can employ several strategies:

• Use a specialized method: The MultiSecant method is recommended as a robust alternative that comes at no extra cost per SCF cycle compared to DIIS [11].
• Apply a finite electronic temperature: Smearing the Fermi level helps to dampen charge oscillations and can significantly improve convergence [9].
• Adopt more conservative mixing parameters: Reducing the SCF%Mixing parameter and/or the DIIS%Dimix parameter can stabilize the SCF procedure [11].
• Try the Periodic Pulay method: This generalization of DIIS, which performs Pulay extrapolation only at periodic intervals while using linear mixing in between, has been shown to enhance both robustness and efficiency [21].

Q3: My calculation converged, but the S² expectation value is wrong. What does this mean?

In an unrestricted calculation (UHF or UKS), the wave function is a single determinant that is not necessarily an eigenfunction of the S² operator. Therefore, it can be a mixture of spin states (e.g., singlet and triplet), leading to an non-integer expectation value of S² [39]. This is a inherent property of the method and not an error in convergence. If a pure spin state is required, a Restricted Open-Shell (ROSCF) calculation should be considered where applicable [39].

Q4: What is the practical difference between the DIIS and MultiSecant methods in terms of computational overhead?

A key advantage of the MultiSecant method is that it provides improved robustness without increasing the cost per SCF iteration compared to the standard DIIS method [11]. This makes it an attractive drop-in replacement for problematic systems. In contrast, some other advanced methods, like the Quadratic Convergent SCF (QCSCF), are more computationally expensive [9].

---

Experimental Protocols for Method Benchmarking

Protocol 1: Benchmarking Robustness Across Diverse Systems

• System Selection: Construct a test set that includes a variety of materials: small molecules (e.g., Hâ‚‚O), semiconductors (e.g., Si), and metal clusters (e.g., Pd clusters or an Fe slab) [9] [11].
• Method Configuration: Perform SCF calculations on all systems using the methods to be compared (e.g., standard DIIS, MultiSecant, Periodic Pulay). Use the same initial guesses and convergence criteria for all.
• Metric Tracking: For each run, record (1) the success/failure of convergence within a set number of iterations, and (2) the number of SCF iterations required.
• Analysis: Compare the success rates and average iteration counts across the different system types to assess the robustness of each method.

Protocol 2: Evaluating Convergence Speed and Computational Cost

• Single System Focus: Choose a known problematic system, such as a metallic slab [11].
• Controlled Calculation: Run the calculation to convergence using different convergence acceleration methods.
• Data Collection: For each method, meticulously record:
  • The total number of SCF cycles.
  • The wall-clock time to convergence.
  • The peak memory usage and any disk I/O overhead.
• Comparison: Normalize the data against the simplest method (e.g., linear mixing) to determine the speedup factor and identify any additional computational overhead.

---

Quantitative Metrics for SCF Convergence Analysis

Table 1: Key Performance Indicators for SCF Convergence Methods

Metric Category	Specific Metric	Description & Measurement
Robustness	Success Rate	Percentage of test systems that converge to the specified threshold (e.g., 10⁻⁵ a.u. maximum DIIS error [25]).
	Stability	Ability to converge without manual intervention (e.g., reducing mixing parameters).
Speed	Iteration Count	Total number of SCF cycles required to reach convergence.
	Wall-Time	Actual computational time taken.
Computational Overhead	Cost per Iteration	CPU time, memory, and disk usage for a single SCF cycle.
	Storage Requirements	Size of the DIIS/MultiSecant subspace (e.g., default of 15-20 Fock/Density matrices [9] [25]).

Table 2: Research Reagent Solutions for SCF Troubleshooting

Reagent (Software Feature)	Function	Example Usage
Kerker Preconditioner	Damps long-wavelength charge oscillations in plane-wave codes; inspires similar techniques for Gaussian bases [9].	Essential for metallic systems to counteract charge sloshing [9].
Fermi-Dirac Smearing	Smears electronic occupation around the Fermi level, reducing sharp changes in the density [9].	SCF%ElectronicTemperature 0.001 (in Hartree) to improve metal convergence [11].
DIIS Subspace Size	Controls the number of previous iterations used for extrapolation [25].	DIIS_SUBSPACE_SIZE 20 (default is often 15). A larger subspace can help but may become ill-conditioned [25].
Mixing Parameter	Determines the fraction of the new output density used in the next input density.	SCF%Mixing 0.05 for a more conservative, stable convergence in difficult cases [11].

---

Method Selection and Workflow Diagram

---

Advanced Technical Reference

The DIIS Error Metric The core of the DIIS method is the definition of an error vector, eᵢ, which measures the degree of non-self-consistency at iteration i. For a density matrix P and Fock matrix F, this error is typically defined by the commutation relation [25]: eᵢ = SPᵢFᵢ - FᵢPᵢS where S is the overlap matrix. At convergence, this commutator should be zero. DIIS works by finding a linear combination of previous Fock matrices that minimizes the norm of this error vector within a defined subspace [25]. The convergence criterion is often that the largest element of this error vector is below a cutoff, for example, 10⁻⁵ a.u. for single-point energies [25].

Periodic Pulay Algorithm The Periodic Pulay method is a simple but powerful modification to the standard DIIS (Pulay) method. The algorithm can be summarized as follows [21]:

• For a predetermined number of SCF iterations (e.g., m iterations), use a simple linear mixing scheme: ρᵢ₊₁ = ρᵢ + β * f(ρᵢ), where β is the mixing parameter.
• After every m linear mixing steps, perform a single Pulay extrapolation step using the history of iterations stored in the DIIS subspace.
• Repeat until convergence is achieved. This intermittent use of Pulay extrapolation has been shown to significantly improve the robustness of the convergence process for a wide range of systems, including those where standard DIIS fails [21].

FAQs: Troubleshooting SCF Convergence

1. Why does my SCF calculation for an open-shell transition metal complex oscillate or fail to converge?

Open-shell transition metal systems are notoriously difficult to converge due to their complex electronic structures with near-degenerate orbital energies [1]. This can cause large fluctuations in the initial SCF iterations. To stabilize convergence:

• Apply Damping or Level Shifting: Use keywords like SlowConv or VerySlowConv to introduce damping, which reduces the influence of large changes in the density matrix between iterations [1]. Level shifting can also be effective [1].

• Use a Robust Algorithm: Switch to a second-order convergence method like the Trust Radius Augmented Hessian (TRAH) or try the KDIIS algorithm, sometimes in combination with the SOSCF method [1].
• Improve Initial Guess: Converge a simpler calculation (e.g., with a smaller basis set like SZ or a different functional like BP86) and use its orbitals as a guess for the more complex calculation via MORead [1] [11]. Alternatively, try converging a closed-shell oxidized state and use its orbitals [1].

2. What immediate steps should I take when a standard DIIS calculation fails on a metallic surface?

Metallic systems, such as Pd or Fe slabs, often have small or no band gaps, which can lead to charge sloshing and convergence issues [11] [40].

• Use Conservative Mixing: Reduce the mixing parameter in the SCF cycle to dampen the updates to the density [11].

• Switch to MultiSecant or LIST Methods: The MultiSecant method is a robust alternative to DIIS that comes at no extra cost per SCF cycle [11]. The LIST or LISTi methods can also be effective, though they may increase the cost per iteration [11].

• Adjust DIIS Parameters: Make the DIIS procedure more conservative by decreasing the DIIS%DiMix parameter [11]. For pathological cases, increasing the number of previous Fock matrices used in the DIIS extrapolation (DIISMaxEq) can help [1].

3. How can I force a calculation to continue after near SCF convergence, and when is this advisable?

Most quantum chemistry programs will stop or behave differently if the SCF cycle does not fully converge. This behavior can sometimes be modified.

• For Single-Point Calculations: The default in programs like ORCA is to stop after SCF non-convergence to prevent using unreliable results. You can override this with a keyword like SCFConvergenceForced or %scf ConvForced true end, but this is not generally recommended [1].
• For Geometry Optimizations: The default behavior is often more lenient. ORCA, for example, will continue an optimization if "near SCF convergence" is achieved, as minor issues in early steps may resolve as the geometry improves [1]. Use SCFConvergenceForced if you want to insist on full convergence at every step [1].

4. What are the key differences between DIIS and MultiSecant methods for difficult systems?

The following table summarizes the core characteristics of these two algorithms:

Feature	DIIS (Direct Inversion in the Iterative Subspace)	MultiSecant
Core Principle	Extrapolates a new Fock matrix by minimizing the error vector norm using a linear combination of previous matrices [18].	A quasi-Newton method that builds an approximate Hessian to guide convergence [11].
Computational Cost	Low cost per iteration [11].	Comparable cost per iteration to DIIS [11].
Convergence Robustness	Can be fast but may oscillate or fail for pathological systems; prone to ill-conditioning [18] [1].	Often more robust and reliable for difficult systems like metals and open-shell complexes [11].
Typical Use Case	Default choice for well-behaved systems (e.g., closed-shell organic molecules).	Recommended when DIIS fails or struggles [11].

5. My calculation halts due to "dependent basis." What does this mean and how can I fix it?

This error indicates that the basis set used is nearly linearly dependent, which jeopardizes numerical accuracy [11].

• Do Not Relax the Criterion: It is not advisable to simply loosen the linear dependency tolerance, as this can lead to incorrect results [11].
• Use Confinement: A common cause is overly diffuse basis functions. Applying spatial confinement to the basis functions, especially for atoms in the interior of a slab or cluster, can reduce their range and eliminate the dependency [11].
• Remove Basis Functions: As a last resort, manually removing the most diffuse basis functions from the set can resolve the issue [11].

Experimental Protocols for Converging Pathological Systems

Protocol 1: Advanced DIIS with Damping for Open-Shell Clusters This protocol is designed for systems like iron-sulfur clusters where standard methods fail [1].

• Initial Setup: Use the SlowConv keyword to introduce strong damping.
• SCF Configuration: Apply the following settings to tightly control the DIIS procedure.

• Initial Guess: Employ a PAtom or Hueckel guess if the default fails.
• Restart: If the calculation trails off near convergence, restart it using the orbitals from the last successful step.

Protocol 2: MultiSecant Setup for Metallic Slabs This protocol leverages the robustness of the MultiSecant method for metallic systems [11].

• Method Selection: In the input, specify the SCF method as MultiSecant.

• Conservative Convergence: Combine this with a tighter numerical integration grid to improve precision, which is often a hidden cause of convergence problems.

• Two-Step Strategy: If the system is very large, first converge with a minimal basis set (e.g., SZ), then use the resulting density or orbitals as a starting point for a calculation with the full target basis set [11].

Protocol 3: Automated Workflow for Geometry Optimizations This protocol uses adaptive settings during a geometry optimization to improve efficiency [11].

• Define Automation: In the geometry optimization block, set rules to change SCF parameters based on the optimization cycle or gradient size.
• Sample Automation Code:
  This allows for faster, looser SCF cycles when the geometry is poor and forces tight, accurate cycles as the geometry approaches convergence [11].

The Scientist's Toolkit: Research Reagent Solutions

The table below lists key computational "reagents" and their roles in managing SCF convergence.

Item	Function	Application Context
Damping (SlowConv)	Reduces the weight of new Fock matrix updates, stabilizing oscillations [1].	Early SCF cycles with large fluctuations.
Level Shifting	Shifts virtual orbital energies to reduce mixing with occupied orbitals, aiding convergence [1].	Systems where orbital near-degeneracies cause problems.
DIIS Subspace Size (DIISMaxEq)	Number of previous Fock matrices used for extrapolation. A larger subspace can aid convergence in difficult cases [18] [1].	When standard DIIS (with ~5 matrices) is insufficient.
MultiSecant Algorithm	A robust, quasi-Newton SCF solver that is often more reliable than DIIS [11].	Primary method for metals or fallback when DIIS fails.
Electronic Temperature	Smears orbital occupations, facilitating convergence in metallic and small-gap systems [11].	Metals and systems with challenging orbital degeneracies.
High-Quality Grid / Numerical Accuracy	Improves the precision of integral calculations, removing numerical noise that hinders convergence [11].	When convergence issues are due to numerical inaccuracies.

SCF Troubleshooting Workflow

The following diagram outlines a logical decision pathway for addressing SCF convergence problems, integrating the DIIS and MultiSecant methods within a broader research strategy.

Troubleshooting Guide: Advanced SCF Convergence

Frequently Asked Questions

1. My SCF calculation for a system with a very small HOMO-LUMO gap is not converging, even with DIIS. What are my options?

For systems with small HOMO-LUMO gaps or near-degenerate states, consider these alternative algorithms:

• EDIIS (Energy-DIIS): Often provides more stable convergence for systems where standard DIIS fails due to electronic structure challenges.
• ARH (Augmented Roothaan-Hall): A robust alternative that directly minimizes the total energy as a function of the density matrix using a preconditioned conjugate-gradient method with a trust-radius approach. This method can be viable for difficult systems where other accelerators fail [4].
• MESA and LISTi: Additional convergence acceleration methods that may show significantly different convergence behaviors for various chemical systems [4].

2. How can I modify DIIS parameters to improve convergence in problematic cases?

For a slow but steady SCF iteration of a difficult system, use these parameter values as a starting point [4]:

Parameter	Recommended Value	Purpose
N (DIIS expansion vectors)	25	Increases iteration stability
Cyc (initial SCF steps before DIIS starts)	30	Allows for initial equilibration
Mixing	0.015	Provides more stable iteration
Mixing1 (first cycle mixing)	0.09	Gentle start for problematic cases

Implementation example:

3. What non-DIIS techniques can help with SCF convergence problems?

Two primary techniques can assist, though they slightly alter end results:

• Electron Smearing: Simulates a finite electron temperature using fractional occupation numbers to distribute electrons over multiple near-degenerate levels. Keep values as low as possible, using multiple restarts with successively smaller smearing values [4].
• Level Shifting: Artificially raises the energy of unoccupied virtual orbitals. Note: this technique gives incorrect values for properties involving virtual levels (excitation energies, response properties, NMR shifts) and may inadequately describe metallic systems with vanishing HOMO-LUMO gaps [4].

Experimental Protocols for SCF Method Comparison

Protocol 1: Systematic Evaluation of Convergence Accelerators

Objective: Compare the performance of DIIS, EDIIS, and ARH methods on pathological molecular systems.

Methodology:

• Select test systems representing common convergence challenges: transition metal complexes with localized open-shell configurations, systems with dissociating bonds, and molecules with small HOMO-LUMO gaps.
• Use consistent initial guesses for all methods (linear combinations of atomic configurations).
• Implement each algorithm with optimized parameters:
  • DIIS: Use both standard (N=10, Mixing=0.2) and conservative (N=25, Mixing=0.015) parameters
  • ARH: Apply preconditioned conjugate-gradient method with trust-radius
  • EDIIS: Implement energy-based convergence criteria
• Measure convergence using: number of iterations, computational time, residual error evolution, and final total energy stability.

Expected Outcomes: Quantitative comparison of method performance across different system types, enabling recommendation of optimal strategies for specific electronic structure challenges.

Validation: For each converged result, verify stability through molecular property calculations and orbital analysis to ensure physical meaningfulness of the solution.

Research Reagent Solutions: Computational Tools

Tool Name	Function	Application Context
DIIS Algorithm	Convergence acceleration using iterative subspace methods	Standard SCF procedures for well-behaved systems
EDIIS Variant	Energy-based convergence criteria	Systems where conventional DIIS oscillates
ARH Method	Direct energy minimization via conjugate-gradient	Difficult systems with convergence problems [4]
MESA Accelerator	Alternative convergence algorithm	Specific chemical systems where DIIS underperforms [4]
LISTi Method	Additional convergence option	Variety of challenging chemical systems [4]
Electron Smearing	Fractional occupation of orbitals	Metallic systems or those with near-degenerate states [4]
Level Shifting	Virtual orbital energy manipulation	Problematic cases (with property calculation limitations) [4]

SCF Convergence Decision Pathway

Advanced Algorithm Implementation Parameters

Table: Comparative SCF Acceleration Method Performance

Method	Computational Cost	Stability	Best For	Key Parameters
Standard DIIS	Low	Moderate	Well-behaved systems	N=10, Mixing=0.2, Cyc=5
Conservative DIIS	Low	High	Problematic systems	N=25, Mixing=0.015, Cyc=30 [4]
EDIIS	Moderate	High	Oscillating systems	Energy-based criteria
ARH	High	Very High	Difficult convergence cases	Trust-radius, conjugate-gradient [4]
MESA	Moderate	Variable	Specific system types	Method-dependent parameters [4]
LISTi	Moderate	Variable	Various challenging systems	Method-dependent parameters [4]

Implementation Notes for ARH: The Augmented Roothaan-Hall method represents a fundamentally different approach from DIIS-based methods, as it directly minimizes the total energy rather than accelerating the traditional SCF procedure. This makes it particularly valuable for systems where the electronic configuration is far from any stationary point or where standard methods show strongly fluctuating errors [4].

Frequently Asked Questions

What is the primary cause of SCF convergence failures? SCF convergence failures typically arise from a combination of factors, including an unsuitable initial guess, large charge oscillations, and the presence of nearly degenerate energy levels (a small HOMO-LUMO gap). This is particularly common in metallic systems, open-shell transition metal complexes, and systems described with diffuse basis sets [9] [1]. The algorithm's inability to effectively damp these oscillations or handle near-degeneracies leads to a diverging or stagnating SCF procedure.

My calculation is for a geometry optimization. Should I use tight SCF convergence from the start? No. It is often computationally efficient to use a more lenient SCF convergence criterion at the beginning of a geometry optimization when the nuclear gradients are still large. As the geometry approaches a minimum, the convergence criterion should be tightened. This can be automated in some software packages [11]. For example, you can start with a Convergence%Criterion of 1.0e-3 and gradually tighten it to 1.0e-6 over the first 10 geometry iterations.

When should I consider alternatives to the standard DIIS algorithm? You should consider alternatives like MultiSecant, Geometric Direct Minimization (GDM), or second-order methods when:

• Standard DIIS leads to large oscillations in the energy or density in the first few iterations [11] [1].
• You are studying a metallic system or a molecule with a very small band gap [9].
• You are calculating an open-shell system, especially one containing transition metals [1].
• DIIS converges to a false solution, which can sometimes be detected if the alpha and beta spin error vectors cancel each other out [41] [25].

Troubleshooting Guide: Solving SCF Convergence Problems

This guide provides a step-by-step protocol to diagnose and resolve persistent SCF convergence issues.

Step 1: The Initial Check Before altering algorithms, verify the fundamentals.

• Inspect Geometry: Ensure your molecular geometry is physically reasonable. Unrealistic bond lengths or angles can prevent convergence [1].
• Check Basis Set: Large, diffuse basis sets can lead to linear dependence. Use confinement or remove the most diffuse functions to mitigate this [11].
• Verify Numerical Settings: In DFT calculations, insufficient integration grid quality can cause convergence failure. Increasing the grid size can help [1].

Step 2: Conservative Stabilization If the SCF shows large oscillations, your first action should be to increase damping.

• Action: Reduce the SCF mixing parameter. For instance, change SCF%Mixing from a default of 0.075 to 0.05 or lower [11].
• Rationale: This strongly damps the update of the density or Fock matrix between cycles, smoothing out oscillations.

Step 3: Algorithm Switching and Tuning If damping is insufficient, the core strategy is to select a more robust algorithm.

• For general robustness: Switch from DIIS to the MultiSecant method. This method often converges at a similar cost per cycle but is more stable for problematic systems [11].

• For severe oscillations and open-shell systems: Use the Geometric Direct Minimization (GDM) algorithm. GDM properly accounts for the curved geometry of the orbital rotation space, making it very robust, though sometimes slower than DIIS [41].
• For pathological cases (e.g., metal clusters): Implement a combined strategy. Apply a finite electronic temperature (e.g., Convergence%ElectronicTemperature 0.001) to smear orbital occupations and combine it with a robust algorithm like GDM or a large DIIS subspace [11] [9] [1].

Step 4: Advanced Interventions For systems that remain non-convergent, more expensive options are available.

• Use a Better Initial Guess: Instead of the default guess, try initializing the density using core Hamiltonian orbitals (HCore) or by reading converged orbitals from a simpler, previously converged calculation (e.g., using a smaller basis set or a different functional) [1].
• Enable Second-Order Convergence: Algorithms like the Trust Region Augmented Hessian (TRAH) use second-derivative information (the Hessian) for highly stable convergence, though at a greater computational cost per iteration. This is often a last resort but is highly effective [3].

The Scientist's Toolkit

Table 1: Key SCF Convergence Algorithms and Their Applications

Algorithm	Best For	Mechanism	Key Input / Control
DIIS (Default)	Closed-shell systems with a good initial guess [41].	Extrapolates a new Fock matrix from a linear combination of previous matrices to minimize the commutator error [41] [25].	DIIS_SUBSPACE_SIZE [41] [25]
MultiSecant	General purpose robust alternative to DIIS at no extra cost [11].	A root-finding method that can be more stable than DIIS for certain problems.	SCF Method = MultiSecant [11]
GDM	Open-shell systems, transition metal complexes, and as a fallback when DIIS fails [41] [1].	Takes optimal steps on the curved hypersphere of orbital rotations to minimize the energy directly [41].	SCF_ALGORITHM = GDM [41]
TRAH / SOSCF	Pathological cases where first-order methods fail [1] [3].	A second-order method that uses an approximate orbital Hessian to achieve quadratic convergence [3].	!TRAH or !SOSCF [1] [3]

Table 2: Essential Parameters for Troubleshooting

Parameter	Function	Action for Poor Convergence
Mixing / Damping	Controls how much of the new Fock/Density is mixed with the old.	Decrease the value (e.g., to 0.05) to stabilize oscillations [11].
DIIS Subspace Size	Number of previous Fock matrices used for extrapolation.	Increase (e.g., to 15-40) for difficult cases [41] [1].
Electronic Temperature	Smears orbital occupations around the Fermi level.	Apply a small value (e.g., 0.001-0.01 Ha) to handle near-degeneracies [11] [9].
Max SCF Iterations	The maximum number of SCF cycles allowed.	Increase if convergence is slow but steady [7] [1].

Experimental Protocol: Systematic SCF Convergence

Objective: To achieve SCF convergence for a difficult open-shell transition metal system.

• Preliminary Calculation:

  • Perform a single-point energy calculation using a fast, robust method (e.g., BP86/def2-SVP) and !SlowConv keyword to generate an initial set of molecular orbitals [1].

• Primary Calculation:

  • Use the orbitals from step 1 as the initial guess for your target level of theory (e.g., a hybrid functional and larger basis set).
  • In the input, specify:
    This utilizes damping and allows a sufficient number of cycles.

• Algorithmic Intervention:

  • If the primary calculation fails, switch to the Geometric Direct Minimization (GDM) algorithm.
  • Alternatively, if using software that supports it, enable the Trust Region Augmented Hessian (TRAH) method, which may activate automatically after failed DIIS cycles [3].

• Final Refinement:

  • Once a converged solution is found, perform a final single-point calculation with a tight convergence criterion (e.g., !TightSCF) and zero electronic temperature to obtain the precise ground-state energy [3].

The following workflow diagram summarizes the logical decision process for selecting an SCF algorithm based on system properties and research goals, as detailed in this article.

Conclusion

The choice between MultiSecant and DIIS methods for SCF convergence is not a one-size-fits-all decision but a strategic one, heavily dependent on the specific chemical system and computational goals. DIIS often provides aggressive and fast convergence for well-behaved systems, while MultiSecant offers enhanced stability for problematic cases with small gaps or complex potential energy surfaces, such as those frequently encountered in drug development involving surface interactions and transition metal catalysts. A deep understanding of both algorithms' parameters—such as DIIS subspace size and MultiSecant's mixing coefficients—is crucial for effective troubleshooting. Future directions should focus on the development of intelligent, adaptive algorithms that automatically select and hybridize these methods, and on their rigorous benchmarking for large-scale biological systems. This will further enhance the reliability and predictive power of computational chemistry in accelerating biomedical discovery and clinical translation.

References

• 1. SCF Convergence Issues - ORCA Input Library [https://sites.google.com/site/orcainputlibrary/scf-convergence-issues]
• 2. Methods to Solve the SCF not Converged | Zhe WANG, Ph.D. [https://wongzit.github.io/method-to-solve-the-scf-not-converged/]
• 3. 7.7. SCF Convergence - ORCA 6.0 Manual [https://www.faccts.de/docs/orca/6.0/manual/contents/detailed/scfconv.html]
• 4. SCF Convergence Guidelines for ADF - SCM [https://www.scm.com/doc/ADF/Rec_problems_questions/SCF.html]
• 5. 4.6 Converging SCF Calculations [https://manual.q-chem.com/5.0/sect-convergence.html]
• 6. 4.5.10 Small-Gap Systems‣ 4.5 Converging SCF Calculations ‣ Chapter 4 Self-Consistent Field Ground-State Methods ‣ Q-Chem 5.2 User’s Manual [https://manual.q-chem.com/5.2/Ch4.S5.SS10.html]
• 7. Self Consistent Field (SCF) — BAND 2025.1 documentation [https://www.scm.com/doc/BAND/Accuracy_and_Efficiency/SCF.html]
• 8. An accurate and efficient framework for modelling the ... [https://www.nature.com/articles/s41557-025-01884-y]
• 9. Improving DIIS convergence for metallic systems using ... [https://www.sciencedirect.com/science/article/abs/pii/S0009261415004911]
• 10. How to solve SCF convergence issues when running a ... [https://www.bragitoff.com/2023/03/how-to-solve-scf-convergence-issues-when-running-a-dft-hf-calculation-solved/]
• 11. Troubleshooting — BAND 2025.1 documentation - SCM [https://www.scm.com/doc/BAND/Troubleshooting/Trouble_Shooting.html]
• 12. 4.5.3 Direct Inversion in the Iterative Subspace (DIIS) [https://manual.q-chem.com/5.4/sect_diis.html]
• 13. Common Errors in Density-Functional Theory - Rowan Scientific [https://rowansci.com/blog/dft-errors]
• 14. DIIS - Wikipedia [https://en.wikipedia.org/wiki/Pulay_mixing]
• 15. Application of the DIIS technique to improve ... [https://www.sciencedirect.com/science/article/abs/pii/S0166128001005024]
• 16. Structure optimization - VASP Wiki [https://www.vasp.at/wiki/index.php/Structure_optimization]
• 17. Second-Order Quasi-Newton Algorithm [https://www.emergentmind.com/topics/second-order-quasi-newton-algorithm]
• 18. 4.5.3 Direct Inversion in the Iterative Subspace (DIIS) [https://manual.q-chem.com/6.3/sect_diis.html]
• 19. 4.5.9 Internal Stability Analysis and Automated Correction ... [https://manual.q-chem.com/5.2/Ch4.S5.SS9.html]
• 20. CP2K — PLAMS 2025.1 documentation - SCM [https://www.scm.com/doc/plams/interfaces/cp2k.html]
• 21. Periodic Pulay method for robust and efficient convergence ... [https://www.sciencedirect.com/science/article/abs/pii/S0009261416000464]
• 22. A Story of Three Levels of Sophistication in SCF/KS-DFT ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10983011/]
• 23. Self-Consistent Field using Direct Inversion in Iterative ... [https://www.sciencedirect.com/science/article/abs/pii/B9780128005361000046]
• 24. Self-Consistent Field Iteration [https://www.emergentmind.com/topics/self-consistent-field-iteration]
• 25. 4.5.3 Direct Inversion in the Iterative Subspace (DIIS) [https://manual.q-chem.com/5.2/Ch4.S5.SS3.html]
• 26. MIXING — CP2K documentation [https://manual.cp2k.org/trunk/CP2K_INPUT/FORCE_EVAL/DFT/SCF/MIXING.html]
• 27. CP2K_INPUT / FORCE_EVAL / DFT / SCF / MIXING [https://manual.cp2k.org/cp2k-4_1-branch/CP2K_INPUT/FORCE_EVAL/DFT/SCF/MIXING.html]
• 28. 4.5.4 Damping‣ 4.5 Converging SCF Calculations ... [https://manual.q-chem.com/5.3/sect_damp.html]
• 29. Electronic structure factors and the importance of ... [https://www.nature.com/articles/s41524-022-00846-z]
• 30. Three-temperature model for predicting critical ... [https://www.nature.com/articles/s41524-025-01798-w]
• 31. Accelerating self-consistent field convergence with the augmented... [https://pubmed.ncbi.nlm.nih.gov/20136307/]
• 32. Delocalization error poisons the density-functional many-body ... [https://pubs.rsc.org/en/content/articlehtml/2024/sc/d4sc05955g]
• 33. Dealing with Spin Contamination - Dr. Joaquin Barroso's Blog [https://joaquinbarroso.com/2017/06/20/dealing-with-spin-contamination/]
• 34. Facing problem in spin contamination [https://talk.q-chem.com/t/facing-problem-in-spin-contamination/1113]
• 35. Scaling and logic in the color code on a superconducting ... [https://arxiv.org/html/2412.14256v1]
• 36. Researchers Take a 'Colorful' Approach to Error Correction ... [https://thequantuminsider.com/2024/12/22/researchers-take-a-colorful-approach-to-error-correction-to-bring-fault-tolerant-quantum-computing-a-step-closer/]
• 37. Adsorption energies on transition metal surfaces [https://www.nature.com/articles/s41467-022-34507-y]
• 38. Toward a new definition of surface energy for late transition ... [https://pubs.rsc.org/en/content/articlehtml/2023/cp/d2cp04024g]
• 39. Electronic Configuration — ADF 2025.1 documentation - SCM [https://www.scm.com/doc/ADF/Input/Electronic_Configuration.html]
• 40. Ground-state FAQs [https://docs.abinit.org/faq/ground_state/]
• 41. 4.5 Converging SCF Calculations [https://manual.q-chem.com/5.1/sect-convergence.html]